Linear Function - 演算法筆記

Complex Eigenvalue（Under Construction!）

Complex Eigenvalue

Cauchy eigenvalue interlacing theorem
Gershgorin eigenvalue circle theorem

Spectral Projection

https://www.caam.rice.edu/~caam440/chapter1.pdf

https://en.wikipedia.org/wiki/Resolvent_formalism

(A - zI)     pencil
(A - zI)⁻¹   resolvent / spectra
det(A - zI)  characteristic polynomial

(zI - A)⁻¹ = z⁻¹(I + A/z + A²/z² + ...)

特徵值shift-inverse調到無限大，環積分之後變成特徵向量外積(特徵分解外積表示法)
用C圈選隔離特徵值，得到其特徵向量。
特徵值相異，X是向量；特徵值重根，X是正規正交矩陣。
   -1
∫  --- (A - zI)⁻¹ dz = XXᵀ = P     spectral projection
 C 2πi

         A - λⱼI
Pᵢ = pro -------     Lagrange interpolation
     j≠i λᵢ - λⱼ

專著《Eigenvalues of Matrices》

大量特徵值演算法（Sakurai–Sugiura Projection）

《A projection method for generalized eigenvalue problems using numerical integration》

大量特徵值演算法（FEAST）

《A Density Matrix-based Algorithm for Solving Eigenvalue Problems》

《PFEAST: A High Performance Sparse Eigenvalue Solver Using Distributed-Memory Linear Solvers》

Spectral Projection那一坨積分
用積分演算法求得（Gaussian Quadrature？）
複平面，最大最小特徵值的圓，等距取樣。
自己設定半徑，看要圈多少特徵值。
這樣就得到XXᵀ了。

P = XXᵀ不做共軛分解。
而是隨便亂猜X̃，乘在後面(XXᵀ)X̃。
如果猜得準，導致相消剩下X，猜中特徵矩陣。
拿(XXᵀ)X̃來做Rayleigh–Ritz Projection，就這樣。

Generalized Eigenvalue（Under Construction!）

Generalized Eigenvalue

Ax = λBx. if A - zB is singular then z is an eigenvalue.

matrix pencil: A - zB. regular iff det(A - zB) ≠ 0.

B⁻¹A or AB⁻¹ has same eigenvalue.

PₗAPᵣ = λPₗBPᵣx has same eigenvalue.

Weierstrass canonical form:

             [ J-zI |   0  ]
Pₗ(A-zB)Pᵣ = [------+------]
             [   0  | I-zJ ]   below J is nilpotent. diagonal are all 0.

Generalized Schur Decomposition（QZ Decomposition）

A = QSZᵀ
B = QTZᵀ

Biorthogonal Decomposition

biorthogonal decomposition / biorthogonalization

VᵀAW = B    where VᵀW = I

two-side Rayleigh Quotient. generalized eigenvalue. pencil.

VᵀAW
----
 VᵀW

雙正交分解演算法（Unsymmetric Lanczos Iteration）

Lanczos Iteration的時間複雜度實在太銷魂，於是有人硬是用Lanczos Iteration處理一般矩陣。

可以得到三對角線矩陣。

Linear Approximation（Under Construction!）

Linear Approximation【尚無正式名稱】

特徵值絕對值最小者歸零，得到最小平方誤差矩陣。

消滅任一項：該特徵值歸零，該特徵向量不變。維度減一。

消滅特徵值最小項：矩陣元素誤差平方和最小的降維方式。

‖A‖_F² = tr(AᵀA) = tr((sum λᵢPᵢ)ᵀ(sum λᵢPᵢ))
=========== tr(sum λᵢ²Pᵢ) = sum λᵢ² tr(Pᵢ) = sum λᵢ²
when Pᵀ = P aka A is normal

pseudoinverse = projection = least squares = linear regression
= dot product of arbitrary basis

linear approximation
= dot product of othronormal basis

galerkin method: orthonormal basis dot
conjugated gradient method: A-orthonormal residual dot
linear feedback system: time series dot (fixedpoint)
companion matrix: x x^2 x^3 dot (differential equation eigenfunction)
taylor expansion: order-1 to order-n gradient dot

kalman filter: residual dot

https://www.encyclopediaofmath.org/index.php/Galerkin_method
正規正交基底的線性組合的線性變換，分別對各個基底點積。
Ax = A(c1q1 + c2q2 + ...)
q*Ax = c q*Aq   when dot(qi,qj) = 0

點積結果是二次型。正規化之後得到虛擬特徵值，乘上c倍。
c q*Aq/q*q

https://en.wikipedia.org/wiki/QR_decomposition
QR分解之GS正交化　Q當作正規正交基底　R是點積
dot(q,a) = q*a

[galerkin method solve linear equation]
xk = x0 + subspace = x0 + (α0 b + α1 Ab + α2 A²b)
such that dot(b - Axk, q) = 0   餘數通通通過基底q的測試
如果是 linear least squares  應該要改成　min dot(b - Axk, q)

xₜ₊₁ = xₜ - dot(J, F) / dot(J, J)
視作投影公式：F(x)投影到J。
向量投影到梯度，再求得向量到梯度的差距。

can we use them? when use the linearization
1. fixpoint iteration (linear equation)
2. power iteration (linear eigenvalue)

n->n求根   其實就是求特徵值？　power iteration？
           companion matrix? Cayley–Hamilton Theorem?

Linear Approximation（Under Construction!）

Symmetric Matrix

「對稱矩陣」。yᵀAx = xᵀAy。

這是仿照dot(y, Ax) = dot(x, Ay)的概念，幾何意義是兩個向量x與y，無論取哪一個實施線性變換，點積仍相同。

Positive Definite Matrix / Positive Semidefinite Matrix

「正定矩陣」。xᵀAx > 0，不討論x = 0。

「半正定矩陣」。xᵀAx ≥ 0，不討論x = 0。

這是仿照dot(x, Ax) > 0的概念，幾何意義是Ax投影到x上面，投影量總是大於0，無論哪種x。換句話說，向量經過線性變換，轉彎幅度少於±90˚，未達半個面。

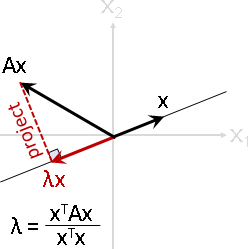
眼尖的讀者應該注意到了，dot(x, Ax)再除以x的長度平方，就是虛擬特徵值。正定矩陣的虛擬特徵值恆正，於是特徵值恆正。

二次型除以x長度平方，換句話說，向量經過線性變換再投影回去，即是「虛擬特徵值Rayleigh Quotient」。

Symmetric Positive Definite Matrix

「對稱正定矩陣」。既對稱，又正定。同時具備兩者性質。

原本定義可以改寫成xᵀAx = xᵀMᵀMx = (Mx)ᵀMx = ‖Mx‖² > 0。代數意義是線性變換之後的長度的平方、恆正。

二次型開根號，換句話說，向量經過線性變換的長度，形成「歐氏長度函數Euclidean Length Function」。

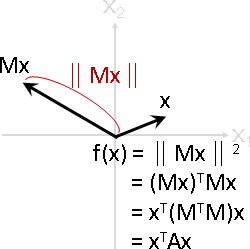
A-orthogonal

「矩陣正交」。yᵀAx = 0。xᵀAy = 0。兩式等價。

Ax與y互相垂直；x經過A變換之後，與y互相垂直。

知名範例：切線速度與加速度互相垂直；一次微分與二次微分互相垂直。

定義y與Ax的內積空間，A必須是對稱正定矩陣。內積空間開根號可以定義距離。

Length / Distance

l(x) = ‖x‖ = √xᵀx   |   d(x,y) = ‖x - y‖ = √(x-y)ᵀ(x-y)
lᴍ(x) = ‖Mx‖        |   dᴍ(x,y) = ‖Mx - My‖ = ‖M(x - y)‖
      = √(Mx)ᵀ(Mx)  |           = √(M(x-y))ᵀ(M(x-y))
      = √xᵀMᵀMx     |           = √(x-y)ᵀMᵀM(x-y)
      = √xᵀAx       |           = √(x-y)ᵀA(x-y)

長度：元素平方和開根號。自己與自己的點積、再開根號。

線性變換之後的長度：恰是二次型開根號，是對稱半正定矩陣。

距離：相減之後的長度。

線性變換之後的距離：宛如二次型開根號，是對稱半正定矩陣。