mathematical morphology
mathematical morphology
Histogram3D[{{0,0},{0,0},{0,0}},{1},Boxed->False,Axes->None]
【註：我製圖技術差，只好介紹陣列版本，而非函數版本。】
調整函數形狀的學問。因為不是顯學，所以名稱矯揉造作，不像一般的數學名詞那樣地簡潔有力。關鍵字 grayscale morphology 。
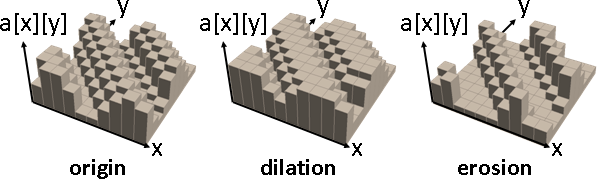
基本操作是 dilation 和 erosion ，進階操作由基本操作組成。
dilation：鄰近格子取最大值。功效是補厚。
erosion：鄰近格子取最小值。功效是削薄。
closing：先 dilation 再 erosion。
opening：先 erosion 再 dilation。
top-hat transform：原函數減掉 opening。
bottom-hat transform：closing 減掉原函數。
鄰近格子可以自訂樣式。另外，大樣式多半可以改為小樣式，效果相同而且時間複雜度更低。
例如 5×5 ，改為兩波 3×3 ，亦得取得 5×5 範圍內的最小值（最大值）。本來讀取 X×Y×5×5 格，變成只讀取 X×Y×3×3×2 格。
運算不可逆、不可抵銷，沒有反運算。個人推測這些運算可以減少亂度。
- const int N = 10;
- int a[N][N]; // 原函數
- int b[N][N]; // 原函數的整形結果
- bool onboard(int i, int j)
- {
- return i >= 0 && i < N && j >= 0 && j < N;
- }
- void dilation()
- {
- for (int i=0; i<N; ++i)
- for (int j=0; j<N; ++j)
- {
- int value = -1e9; // 記錄最大值
- for (int k=0; k<9; ++k) // a[i][j]附近的3x3範圍
- {
- int p = i + (int[]){-1,-1,-1,0,0,0,1,1,1}[k];
- int q = j + (int[]){-1,0,1,-1,0,1,-1,0,1}[k];
- if (!onboard(p, q)) continue;
- if (a[p][q] > value) value = a[p][q];
- }
- b[i][j] = value;
- }
- }
額外使用過濾函數
進階版本。額外設計一個過濾函數。設計不同的過濾函數，得到不同的效果。
窮舉原函數的每個位置；針對一個位置，令過濾函數的中心對準該位置，各個位置點對點相加（相減）後，才取最大值（最小值）。
- const int N = 10;
- int a[N][N]; // 原函數
- int b[N][N]; // 原函數的整形結果
- const int M = 2;
- int m[M][M]; // 過濾函數
- bool onboard(int i, int j)
- {
- return i >= 0 && i < N && j >= 0 && j < N;
- }
- void dilation()
- {
- for (int i=0; i<N; ++i)
- for (int j=0; j<N; ++j)
- {
- int value = -1e9;
- for (int k=0; k<M; ++k)
- for (int l=0; l<M; ++l)
- if (onboard(i+k-M/2, j+l-M/2))
- value = max(value, a[i+k-M/2][j+l-M/2] + m[k][l]);
- b[i][j] = value;
- }
- }
- void erosion()
- {
- for (int i=0; i<N; ++i)
- for (int j=0; j<N; ++j)
- {
- int value = 1e9;
- for (int k=0; k<M; ++k)
- for (int l=0; l<M; ++l)
- if (onboard(i+k-M/2, j+l-M/2))
- value = min(value, a[i+k-M/2][j+l-M/2] - m[k][l]);
- b[i][j] = value;
- }
- }
邏輯運算的版本
不知道為什麼，影像處理教科書非常喜歡討論邏輯運算的版本。數值改成 false 和 true ，最大值（最小值）改成 OR （ AND ），功效是增厚（削薄）圖形的外緣。
UVa 12702