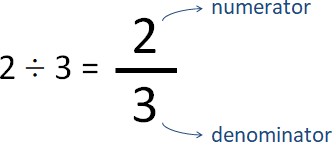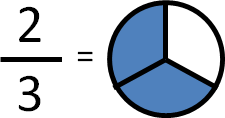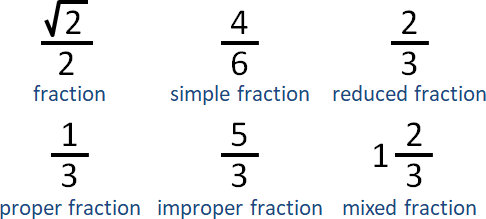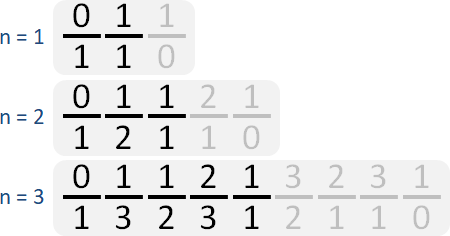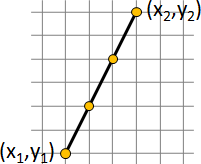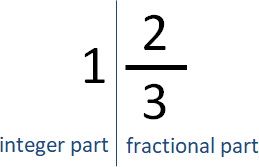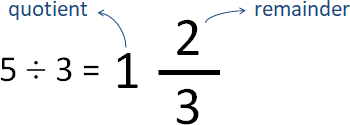fraction

「分數」。兩數相除。上面叫分子、下面叫分母。

fraction可以畫成圖形

教科書喜歡將分數畫成圓餅圖。

fraction類型

分數細分許多類型：

simple fraction：分子分母都是整數。（分母不為0。）
reduced fraction：無法約分。公因數只有1。最大公因數是1。互質。
proper fraction：分子小於分母。
improper fraction：分子大於等於分母。
mixed fraction：一個整數和一個分數。

中文自創另一套類型，細節略有不同：

最簡分數：無法約分。公因數只有1。最大公因數是1。互質。
真分數：分子小於分母。且是最簡分數。
假分數：分子大於等於分母。
帶分數：一個整數和一個分數。

fraction運算

擴分、約分、通分、拆分、四則運算、分母為零，這些我都省略不講。可以嗎？可以吧？

fraction - order

Stern–Brocot tree數列形式

一串數列，最初只有兩個分數0/1和1/0。所有相鄰分數之間，插入新分數：左邊a/b、右邊c/d、中間插入(a+c)/(b+d)。分子相加、分母相加。

不斷遞推下去，理論上涵蓋所有最簡分數，而且不會重複。

一、任意分數gcd(a,b) = 1。通通都是最簡分數。
二、相鄰分數a/b < c/d。數列嚴格遞增。
三、相鄰分數ad - bc = -1。通分、相減、分子恰是-1。

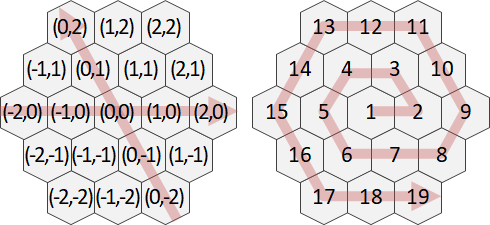
Stern–Brocot tree格點形式

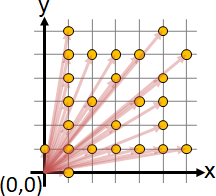
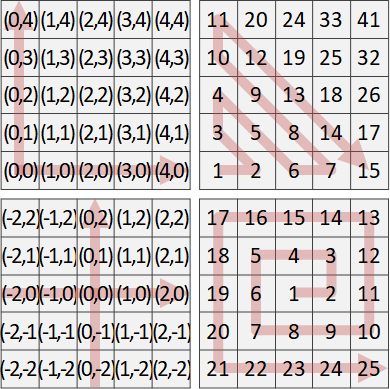
分數變成向量。最初是兩個向量Y軸(0,1)、X軸(1,0)。所有相鄰向量之間插入新向量：向量加法，即是平行四邊形的對角線。

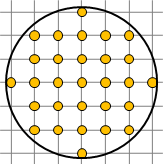
不斷遞推下去，理論上涵蓋所有互質格點，而且不會重複。

一、任意向量gcd(a,b) = 1。一個向量中途不會穿過其他格點。
二、相鄰向量a/b < c/d。斜率嚴格遞減。
三、相鄰向量ad - bc = -1。相鄰向量叉積是-1。三角形面積是1/2。

Stern–Brocot tree二元樹形式

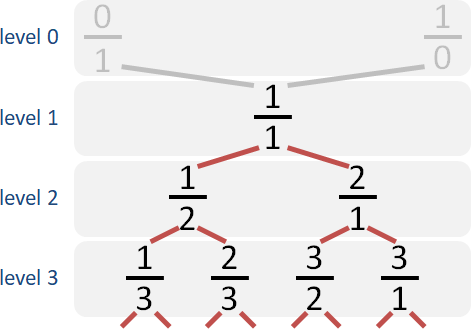
數列們重新繪製成二元搜尋樹。左子樹較小、右子樹較大。

一個分數可以重新表示成一條路徑，例如3/4就是LRR。也可以重新表示成二進位字串，例如3/4就是011。

雖然Stern–Brocot tree的性質非常強悍，但是目前沒有任何演算法使用Stern–Brocot tree。原因可能是數論演算法教科書沒有介紹Stern–Brocot tree，導致發展遲緩。振興任務交給各位了。

UVa 10077 11350

Farey sequence

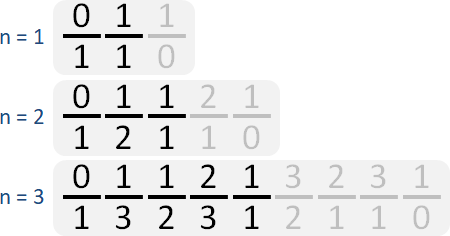
0到1的最簡分數，分子分母小於等於n，從小到大排列。

Stern–Brocot tree的左半邊。就這樣。

UVa 10408 10214

Calkin–Wilf tree

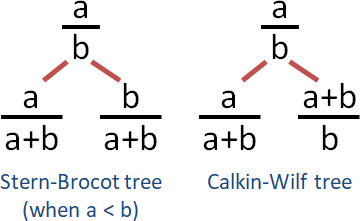
樹根a/b、左小孩a/(a+b)、右小孩(a+b)/b。

Stern–Brocot tree路徑頭尾顛倒。就這樣。

fraction - lattice

lattice points on a line segment

線段上面格點數量。頂點剛好都是格點。

可以用最大公因數求得。

UVa 11768

Pick's theorem

簡單多邊形內部格點數量。頂點剛好都是格點。

數學公式：面積 = 內部格點數量 + 邊界格點數量 / 2 - 1。

簡單多邊形面積：線段向量叉積。

簡單多邊形邊界格點數量：線段上面格點數量。

UVa 10088 143

lattice points under a convex function curve

凸函數曲線下方格點數量。

此演算法源自Euler Project開發團隊，沒有發表為正式的學術論文。網友Min_25重新實作、設計題目，安徽师范大学附属中学朱震霆《一些特殊的数论函数求和问题》稍作改良。我不會證明演算法正確性。

建立一條足夠貼緊曲線上方的折線，讓折線頂點都是格點，讓折線與曲線之間沒有多餘格點。然後用Pick's theorem計算折線下方格點數量。

在Stern–Brocot tree當中搜尋折線向量，盡量找到斜率最小的折線向量。上向量位在曲線上方，下向量穿到曲線下方、但是斜率大於曲線斜率。

時間複雜度可能是O(n^⅓log³(n))甚至O(n^⅓)。

struct Point {int x, y;};

Point operator+(Point a, Point b)
{
	return {a.x + b.x, a.y + b.y};
}

int count(int n)
{
	// f(x) = n / x
	auto over = [&] (Point p) {return p.x * p.y > n;};
	// f′(x) = - n / x²
	auto lesser = [&] (Point p, Point v) {return p.x * p.x * v.y <= -n * v.x;};

int sqrt_n = sqrt(n);
	int cbrt_n = cbrt(n);

// f(x) = n / x，此例當中，曲線沿45°斜線對稱。
	// 從中間開始計算，統計y = sqrt(n)以下格點，節省時間。
	Point P = {n / sqrt_n, sqrt_n + 1};

stack<Point> s;
	s.push({1, 0});		// 上向量
	s.push({1, -1});	// 下向量

int ans = 0;
	while (true)
	{
		// 橫向計數
		Point L, R;
		for (L = s.top(); over(P + L); P = P + L)
			ans -= P.x * L.y + (L.y - 1) * (L.x - 1) / 2;

// 提早結束。剩下的用窮舉法，仍滿足時間複雜度。
		if (P.y <= cbrt_n) break;

// 丟掉多餘的上向量
		s.pop(); R = s.top();
		while (!over(P + R)) {L = R; s.pop(); R = s.top();}

// 在Stern–Brocot tree當中搜尋折線向量
		while (true)
		{
			Point M = L + R;
			if (over(P + M))
				// 盡量找到斜率最小的上向量
				s.push(R = M);
			else
			{
				// + M之後才檢查斜率
				// 導致下一段折線的上下向量，其斜率大於曲線斜率。
				if (lesser(P + M, R)) break;
				L = M;
			}
		}
	}

// 剩下的用窮舉法
	for (int i = 1; i < P.y; ++i) ans += n / i;
	return ans * 2 - sqrt_n * sqrt_n;
}

luogu P6028

Gauss circle problem

圓形內部格點數量。

可以一行一行數，也可以援引方才的演算法。

UVa 356 luogu P2508

visible lattice point problem

格點遮擋視線。站在原點，可以看到多少格點？

四個象限互相對稱。只需觀察第一象限。

等同於找到所有互質格點。等同於互質數計數函數。

演算法請見本站文件「coprime counting function」。

luogu P2158

fraction - coordinate

integer part / fractional part

「整數部分」。帶分數的左邊整數。

「分數部分」。帶分數的右邊分數。

原本數字等於兩者相加。

quotient / remainder

「商數」。整數除法的份數。整數部分。

「餘數」。整數除法的剩下部分。分數部分的分子。

integer part / fractional part

「整數部分」。小數點以左。

「小數部分」。小數點以右。

原本數字等於兩者相加。

floor function / ceiling function

「向下取整函數」或「地板函數」。相等或略小的整數。

「向上取整函數」或「天花板函數」。相等或略大的整數。

兩者合稱取整函數。

輸入是正數，向下取整函數恰好得到整數部分。輸入是負數，向上取整函數才會得到整數部分。

square grid coordinate system

方格地圖，設定座標，設定編號。

UVa 10642 264 880 903

hexagonal grid coordinate system

六角格地圖，設定座標，設定編號。

UVa 209 10161 808 10182 10595 10964

Ulam spiral

方格地圖，螺旋編號，標出質數位置。±45°斜線，特別明顯。原因至今不明。

Gaussian integer / Gaussian prime

我沒有研究。

UVa 960 1415

Tupper's formula

一行數學式子、一個超長整數，創造特殊圖案。

divisibility

「整除性」。判斷是否能整除一個特定數字。

換句話說：判斷一個特定數字是否是因數。

數學家已經發明許多簡易規則，可以快速判斷整除：

1: 缺乏討論意義。
2: 末位數整除2。（個位數是偶數）
3: 所有位數總和，是3的倍數。遞迴下去。
4: 末兩位數整除4。
5: 末位數整除5。
6: 用2和3來判定。
7: 每三位數一組。偶數組總和、奇數組總和，兩者差值，是7的倍數。遞迴下去。
8: 末三位數整除8。
9: 所有位數總和，是9的倍數。遞迴下去。
10: 末位數是0。
11: 偶數位數總和、奇數位數總和，兩者差值，是11的倍數。遞迴下去。

背後原理是scaling method，數字拆開成各種數量級，分別求餘數、求總和。

UVa 10212 10929 11879 10211 10127 10275

trailing 0s of N!

階乘的末位數有多少個零。整除多少個10。整除多少個2與5。統計2與5的因數數量。

UVa 10212 12689

periodicity

periodicity（cycle finding）【查無正式名稱】

「週期性」。重複特定運算，判斷數字重複出現的週期。

換句話說：找到一個特定的自映射函數的循環。

無窮除法：餘數總是小於除數。反覆計算餘數，餘數必定產生循環。
連續乘法：末位數總是小於10。反覆計算乘積，末位數必定產生循環。

UVa 202 10162

階串的週期性【查無正式名稱】

大家可能聽過階加、階乘。現在發明一個新概念叫做階串：

f(1) = 1
f(2) = 12
f(3) = 123
  :     :
f(12) = 123456789101112
  :     :

背後原理是scaling method，輸入拆開成各種數量級，分別實施運算、尋找循環。