容量下限（流量下限）

先前只討論容量上限，並未討論容量下限。

然而，容量下限有個問題。舉例來說，當容量下限形成環，從源點流出一單位水流，即可滿足容量下限：流往環，不斷繞環，原路返回。導致「憑空出現循環水流」的弔詭現象。

大家目前沒有任何對策！因此轉為討論「循環流」：去掉源點匯點，允許憑空出現循環水流。請見後面章節「flow」。

feasible s-t flow（s-t flow）

「可行流」是符合容量限制的流。「可行流」與「流」的定義完全一樣，我們常常省略「可行」兩個字。差別在於多了「可行」之後，我們專注於「找到一個流」，而非「流量是多少」。

想要形成可行流，每條邊、每個點、每個割的流量，必須符合容量限制：

一、邊：流量，大於等於容量下限，小於等於容量上限。
二、點：入流量，大於等於出容量下限，小於等於出容量上限。
　　　　出流量，大於等於入容量下限，小於等於入容量上限。
三、割：同上。

可行流目前沒有演算法。無法處理「憑空出現循環水流」。

maximum s-t flow / minimum s-t flow

有了容量下限，除了討論「最大流」，還可以討論「最小流」。

目前沒有演算法。無法處理「憑空出現循環水流」。

minimum cost maximum s-t flow

每一條管線，除了有容量限制，還有成本（費率）。成本可以是正值（付費）、負值（補貼）、零（沒事）。水流流過管線，必須考慮費用，儘量減少開銷。

一、一段水流流過一條管線的成本：邊的流量乘以成本。

二、一道水流從源點到匯點的成本：路徑上每一條邊，流量乘以成本，求總和。

三、一個流的成本：圖上每一條邊，流量乘以成本，求總和。

「最小成本最大流」。成本最小的最大流，可能有許多個。

UVa 10594 ICPC 5095 3562 8048

演算法

圖上不可有負成本環，避免「憑空出現循環水流」。

一、先找一個最大流。
二、在剩餘圖上，不斷找負成本環，建立迴流降低成本。
　　直到找不到負成本環為止，即是最小成本最大流。

在一個最大流當中，建立一條封閉的迴流，不會影響總流量，也不會違反流量守恆的規則，雖然會浪費容量空間，但是有機會減少總成本。事實上可以證明，剩餘圖沒有負成本環，即是最小成本最大流，證明省略。

尋找負成本環

有三種方式！

負環：運用label correcting algorithm。整個演算法過程中，最多出現C個負成本環，C是最大的管線容量上限；時間複雜度O(VEC)，偽多項式時間。

最小環：照理說是最理想的方式，可以較快達到最小成本最大流。然而，求最小環是NP-complete問題，時間複雜度是指數時間。

最小平均數環：意外的是個不錯的選擇。整個演算法過程中，最多出現O(VE²logV)個最小平均數環；時間複雜度O(V²E³logV)，多項式時間。證明省略。

演算法

圖上不可有負成本環，避免「憑空出現循環水流」。

仿照Ford–Fulkerson algorithm，不斷尋找成本最小的擴充路徑。證明省略。

一開始沒有負成本環，往後就沒有負成本環。

一、一開始的剩餘圖沒有負成本環。

二、成本最小的擴充路徑，擴充之後讓剩餘圖增加了逆向邊（成本隨之變號，增加了負成本邊），但是剩餘圖仍舊沒有負成本環。證明省略。

如此一來，可以確保剩餘圖隨時都能實施最短路徑演算法。

尋找成本最小的擴充路徑

溯洄沖減後，剩餘圖多出許多逆向的負成本邊，因此必須採用允許負邊的最短路徑演算法，例如label correcting algorithm、Floyd–Warshall algorithm。

或者利用Johnson's algorithm的調整權重手法，將負邊調整為非負邊。此時成本最小的擴充路徑就會變成零成本邊，擴充之後的剩餘圖，就不會多出逆向的負成本邊，而是多出逆向的零成本邊！如此一來，就可採用不允許負邊的Dijkstra's algorithm，降低時間複雜度。

一開始圖上可能有負成本邊，預先實施一次label correcting algorithm調整權重，往後就可持續使用Dijkstra's algorithm了。每次實施Dijkstra's algorithm之後，就馬上調整權重。

一、用label correcting algorithm調整權重，讓每條邊的成本為非負值。
二、不斷尋找成本最小的擴充路徑，直到找不到為止：
　甲、用Dijkstra's algorithm尋找成本最小的擴充路徑。
　乙、調整權重，讓每條邊的成本為非負值。
　丙、擴充流量。

找一條擴充路徑需時O(V²)，最多找O(F)條，時間複雜度O(V²F)，偽多項式時間。

找出一個最小成本最大流＋流量＋成本

// edge list + adjacency lists // 起點、終點、剩餘容量、成本 struct Edge {int a, b, r, w;} edge[1000]; int en = 0; vector<int> adj[10]; void addedge(int a, int b, int c, int w) { // 加入一條邊 edge[en] = (Edge){a, b, c, +w}; adj[a].push_back(en++); // 同時也加入反向邊 edge[en] = (Edge){b, a, 0, -w}; adj[b].push_back(en++); } // label correcting algorithm int p[10], d[10]; // 最短路徑樹、最短路徑長度 int index[10]; // 最短路徑樹對應的邊的索引值 bool inqueue[10]; // 記錄各個點是否在queue當中 void MinCostMaxstFlow(int s, int t) { int flow = 0, cost = 0; // 最小成本最大流的流量與成本 while (true) { // 實施 label correcting algorithm， // 從剩餘圖上面，找到成本最小的擴充路徑。 for (int i=0; i<10; ++i) d[i] = 1e9; d[s] = 0; queue<int> Q; Q.push(s); // inqueue[s] = true; while (!Q.empty()) { int a = Q.front(); Q.pop(); inqueue[a] = false; for (int i=0; i<adj[a].size(); ++i) { Edge& e = edge[adj[a][i]]; int b = e.b; if (e.r > 0 && d[a] + e.w < d[b]) { d[b] = d[a] + e.w; p[b] = a; index[b] = adj[a][i]; if (!inqueue[b]) { Q.push(b); inqueue[b] = true; } } } } // 已經找不到擴充路徑 if (d[t] == 1e9) break; // 計算擴充路徑的流量，並且進行擴充。 int df = 1e9; for (int a = t; a != s; a = p[a]) { int i = index[a]; df = min(df, edge[i].r); } for (int a = t; a != s; a = p[a]) { int i = index[a]; edge[i].r -= df; edge[i^1].r += df; } flow += df; cost += df * d[t]; } cout << "最大流的流量是" << flow; cout << "最小成本最大流的成本是" << cost; } typedef int Graph[10][10]; // adjacency matrix Graph C, F, W; // 容量上限、流量、成本 int p[10][10], d[10][10]; // 記錄最短路徑、最短路徑長度 bool floyd_warshall(int s, int t) { /* 初始化Floyd–Warshall algorithm */ for (int i=0; i<10; ++i) for (int j=0; j<10; ++j) p[i][j] = j; for (int i=0; i<10; ++i) d[i][i] = 1e9; for (int i=0; i<10; ++i) for (int j=0; j<10; ++j) { // 看看能不能正向流動 if (F[i][j] < C[i][j]) d[i][j] = min(d[i][j], W[i][j]); // 也看看能不能逆向沖減，成本越小越好。 if (F[j][i] > 0) d[i][j] = min(d[i][j], W[j][i]); // 由於成本為非負值， // 逆向沖減會降低（或不變）擴充路徑的成本， // 正向流動會提高（或不變）擴充路徑的成本， // 一旦可以逆向沖減時，先考慮逆向沖減一定比較好。 } /* 在剩餘圖上，計算出一條成本最小的擴充路徑。 */ for (int k=0; k<10; ++k) for (int i=0; i<10; ++i) for (int j=0; j<10; ++j) if (d[i][k] + d[k][j] < d[i][j]) { d[i][j] = d[i][k] + d[k][j]; p[i][j] = p[i][k]; } /* 找到擴充路徑，就回傳true。 */ return d[s][t] != 1e9; } void MinCostMaxstFlow(int s, int t) { memset(F, 0, sizeof(F)); int flow = 0, cost = 0; // 最小成本最大流的流量與成本 // 不斷找成本最小的擴充路徑，直到找不到為止。 while (floyd_warshall(s, t)) { int df = 1e9, dc = 0; // 計算可以擴充的流量大小 for (int i=s, j=p[s][t]; i!=j; j=p[i=j][t]) // 因為逆向沖減可以降低（或不變）擴充路徑的成本， // 所以如果逆向有流量， // 那麼剛剛找路徑時一定是逆向沖減。 df = min(df, (F[j][i] ? F[j][i] : C[i][j] - F[i][j])); // 進行擴充，順便計算成本。 for (int i=s, j=p[s][t]; i!=j; j=p[i=j][t]) if (F[j][i]) // 因為逆向沖減可以降低（或不變）擴充路徑的成本， // 所以如果逆向有流量， // 那麼剛剛找路徑時一定是逆向沖減。 F[j][i] -= df, dc -= W[j][i]; else F[i][j] += df, dc += W[i][j]; flow += df; cost += df * dc; } cout << "最大流的流量是" << flow; cout << "最小成本最大流的成本是" << cost; } typedef int Graph[10][10]; // adjacency matrix Graph C, F, W; // 容量上限、流量、成本 int p[10], d[10]; // 最短路徑樹、最短路徑長度 int h[10]; // 調權重函數 bool dijkstra(int s, int t) { /* 初始化Dijkstra's algorithm */ memset(p, -1, sizeof(p)); for (int i=0; i<10; ++i) d[i] = 1e9; /* 在剩餘圖上，計算出一條成本最小的擴充路徑。 */ d[s] = 0; p[s] = -s-1; // 切記：最短路徑演算法要跑過每一個點， // 不能遇到終點（匯點）就馬上結束， // 這樣會無法調整每一條邊的權重。 // （至於從源點流不到的點，就不用理它了，反正不影響流量。） // （溯洄沖減後會多出逆向邊。原先流得到的點，沖減之後還是流得到。） for (int k=0; k<10; ++k) { int a = -1, min = 1e9; for (int i=0; i<10; ++i) if (p[i] < 0 && d[i] < min) min = d[a = i]; if (a == -1) break; p[a] = -p[a]-1; for (int i=a, j=0; j<10; ++j) { if (p[j] >= 0) continue; // 先嘗試逆向沖減，可以降低（或不變）成本。 int d1 = d[i] - (W[j][i] + h[j] - h[i]); if (F[j][i] > 0 && d1 < d[j]) d[j] = d1, p[j] = -i-1; // 再嘗試正向流動 int d2 = d[i] + (W[i][j] + h[i] - h[j]); if (F[i][j] < C[i][j] && d2 < d[j]) d[j] = d2, p[j] = -i-1; } } /* 調整剩餘圖的每一條邊（包括逆向邊）的權重成為非負值， 下次就又可以使用Dijkstra's algorithm了。 */ for (int i=0; i<10; ++i) if (h[i] < 1e9) // 從源點流不到的點就不理它了 h[i] += d[i]; // 累加這次的最短路徑長度即可 /* 找到擴充路徑，就回傳true。 */ return p[t] >= 0; } void MinCostMaxstFlow(int s, int t) { memset(F, 0, sizeof(F)); memset(h, 0, sizeof(h)); int flow = 0, cost = 0; // 最小成本最大流的流量與成本 // 不斷找成本最小的擴充路徑，直到找不到為止。 // （假設一開始就沒有負成本邊，不必先調整權重。） while (dijkstra(s, t)) { int df = 1e9, dc = 0; // 計算可以擴充的流量大小 for (int j=t, i=p[t]; i!=j; i=p[j=i]) // 因為逆向沖減可以降低（或不變）擴充路徑的成本， // 所以如果逆向有流量， // 那麼剛剛找路徑時一定是逆向沖減。 df = min(df, (F[j][i] ? F[j][i] : C[i][j] - F[i][j])); // 更新擴充路徑上每一條管線的流量， // 順便計算擴充路徑的成本。 for (int j=t, i=p[t]; i!=j; i=p[j=i]) if (F[j][i]) // 因為逆向沖減可以降低（或不變）擴充路徑的成本， // 所以如果逆向有流量， // 那麼剛剛找路徑時一定是逆向沖減。 F[j][i] -= df, dc -= W[j][i]; else F[i][j] += df, dc += W[i][j]; flow += df; cost += df * dc; } cout << "最大流的流量是" << flow; cout << "最小成本最大流的成本是" << cost; }

演算法

圖上不可有負成本環，避免「憑空出現循環水流」。

仿照Blocking flow algorithm，每回合找到全部的成本最小的擴充路徑。

利用最短路徑長度，調整圖上所有邊的權重成為非負數之後，此時最短路徑上的邊就是零成本邊。在零成本邊所構成的圖當中，找最大流，便可以一次找到全部的成本最小的擴充路徑。

時間複雜度我也不知道。

註記

flow與s-t flow是兩個不同的概念。然而古代人當初定義問題時，卻將兩者都稱作flow，從此之後便混淆不清了。

cut與s-t cut亦有類似情況。古代人當初沒有cut的概念，將s-t cut直接稱作cut。不過自從有人發表cut的演算法之後，眾人便開始注重用詞了。

以下章節，flow譯作「流」或「循環流」，s-t flow譯作「源匯流」。

flow

從現在起，水流不再從源點流到匯點，水流改為不斷循環。

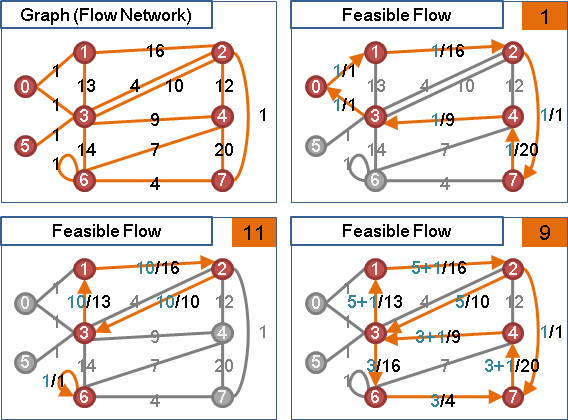
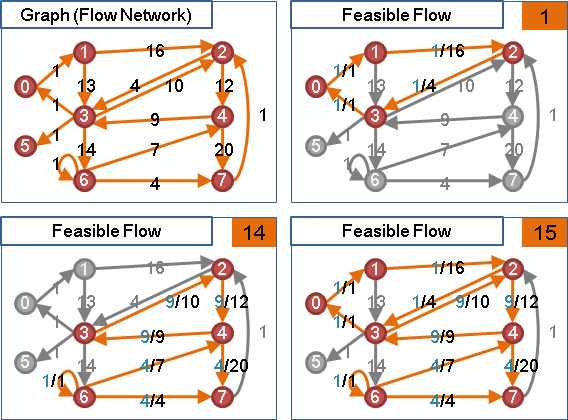
要計算總流量，可將水流分解成數個環，以環流量的總和作為總流量。每次挑一條有水流的邊開始尋找環，最多分解成E個環。

supply / demand

「供點」有水注入、「需點」有水洩出，彷彿源點與匯點。圖上可以有多個供點與需點，供水量總和必須等於需水量總和，才有機會形成可行流。

圖上每一點皆有供需水量：supply的供需水量為正值，該點流出多於流入；demand的供需水量為負值，該點流入多於流出；其他的點的供需水量為零，流入等於流出。

供需水量 = 流出水量 - 流入水量

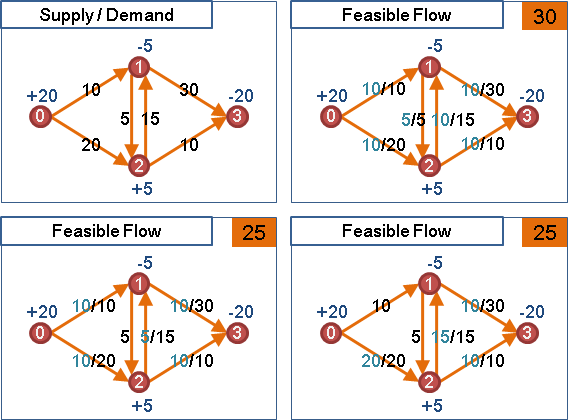
導入supply與demand之後，總流量的定義就不明確了。這裡姑且定義成：supply的總和，再加上不受supply與demand影響的循環流流量。

最大流最小割定理、可行流定理

導入水流流量：任意一個割，甲側流往乙側的水量總和，等於乙側流往甲側的水量總和。

導入容量上限：任意一個割，甲側流往乙側的水量總和，小於等於甲側到乙側的容量總和。最大流流量，小於等於任何一個「管線容量的最小s-t割」！

導入供需水量：任意一個割，甲側的供需水量總和，必須小於等於甲側到乙側的容量總和，才能形成可行流。

導入容量下限：任意一個割，甲側到乙側的容量下限總和，必須小於等於甲側到乙側的容量上限總和、也要小於等於乙側到甲側的容量上限總和，才能形成可行流。

容量下限變成零

有向邊的容量下限，得移轉至supply與demand。

預先流水，水量等於容量下限：

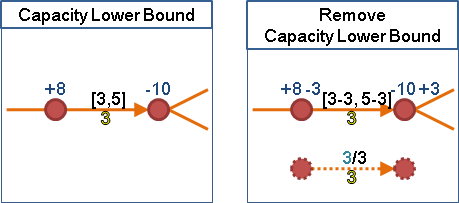
必須記錄每條邊的預流水量與耗費成本，以利之後還原。

容量上限變成無限大

其實沒有必要移除容量上限──最大流演算法皆支援容量上限。不過還是介紹一下吧。

移除容量下限後，可以進一步移除容量上限。容量上限添加至終點，然後回沖：

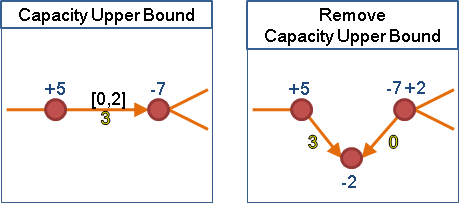
移除容量上限後，變成二分圖，得以設計更簡潔的資料結構與演算法。

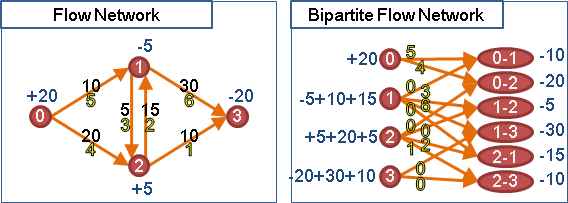
負成本變成正成本

運用溯洄沖減，可以把負成本變成正成本。

預先流水，水量等於容量上限：

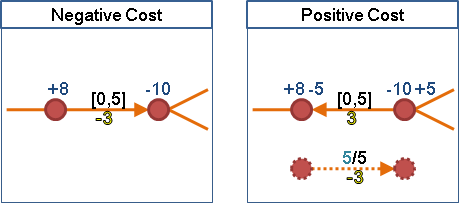
必須記錄每條邊的預流水量和耗費成本，以利之後還原。

無向邊變成有向邊

無向邊得同時雙向流動。一條無向邊可以改為兩條方向相反的有向邊，可是必須共用容量上下限。

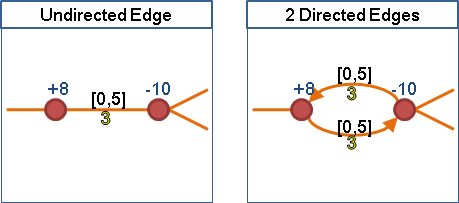
成本非負、沒有容量下限：為了降低成本，來回水流可以變成單向水流。上述兩條方向相反的有向邊，大可不必共用容量上限，宛如普通的有向邊。

成本非負、擁有容量下限：預先在無向邊上來回流動，滿足容量下限。流量是容量下限的一半，可以是0.5。如果流量只能是整數，則可以類比為0/1 knapsack problem，屬於NP-complete問題。

成本為負：同上。流量是實數，就來回流動。流量是整數，NP-complete。

歸約

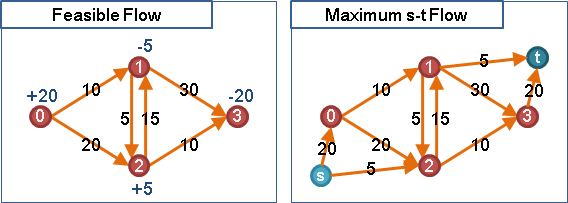
feasible s-t flow -> feasible flow -> maximum s-t flow
導入成本，依然如此。

可行源匯流化作可行循環流。匯點到源點增加一條管線，容量上限無限大（圖上所有邊的容量上限總和），成本無限小。

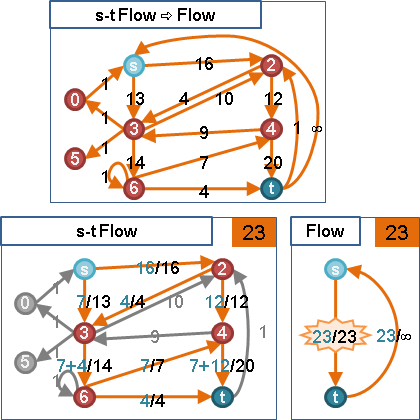
可行循環流化作最大源匯流。新增源點與匯點，源點接至supply，容量上限為供水量；demand接至匯點，容量上限為需水量。然後嘗試求最大源匯流，若源點管線與匯點管線皆滿溢，則有可行循環流，反之則無。拆除新增管線，最大源匯流就變成可行循環流。

總結

流的問題總是可以簡化成：有容量上限、無容量下限、成本非負、有向邊，許多supply和demand。

無論流動方式是循環流、源匯流，無論最佳化目標是最大流、最小流、可行流，都可以歸約成minimum cost maximum s-t flow。

UVa 11647 1259 ICPC 3787 4722 5131

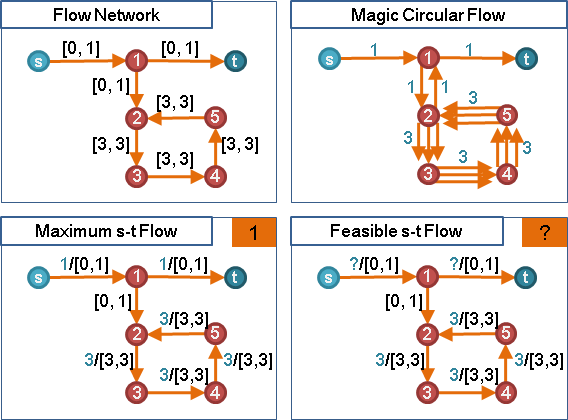
feasible flow

「可行流」。符合供需水量、容量上下限的流。

直覺的方式，就是歸約。進階的方式，就是瞭解歸約過程之後，直接以原圖實施計算，不歸約、不改圖。

承襲maximum s-t flow演算法，額外考慮flow、supply、demand等新概念。

不斷尋找起點為supply、終點為demand的擴充路徑，進行擴充後就根據水量減損supply、增益demand，直到圖上沒有supply與demand為止。

maximum flow

「最大流」。流量最大的可行流。

一、首先隨便找出一個可行流，然後不斷找擴充環。

根據最大流最小割定理，剩餘圖沒有擴充環，即是最大流。

二、窮舉所有兩點之間容量s-t割，取最小值。【尚待確認】

minimum flow

「最小流」。流量最小的可行流。

一、擴充路徑堅持使用點互斥路徑，即得最小流。【尚待確認】

二、首先隨便找出一個可行流，然後不斷消去擴充環。【尚待確認】

我找不到任何有關最小流的正確性證明！

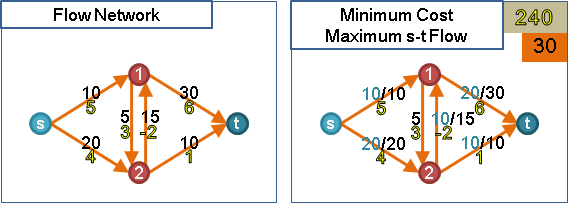
minimum cost flow

「最小成本流」。成本最小的可行流。

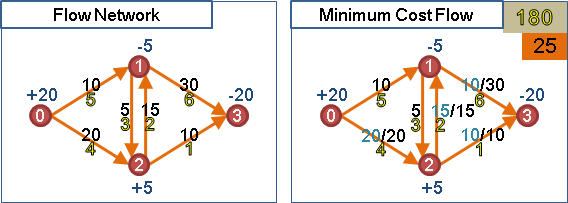
承襲minimum cost maximum s-t flow演算法。

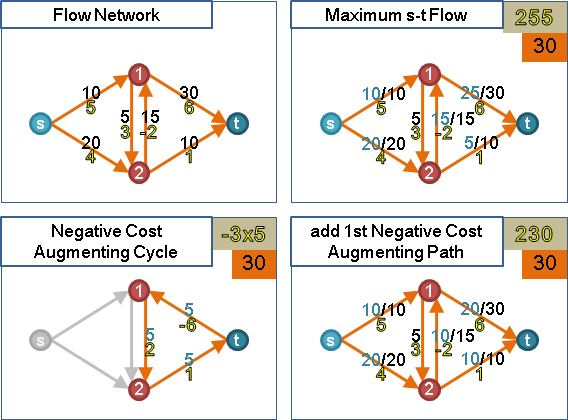
cycle canceling algorithm：先找到任意一個可行流，再以負成本環進行擴充。

successive shortest path algorithm與primal–dual algorithm：不斷尋找起點為excess、終點為deflict、成本最小的擴充路徑，直到所有excess與deflict成為零。如果excess與deflict沒有同時成為零，則沒有可行流。

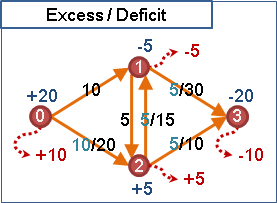
excess / deficit

「積水點」水量超出平衡，「缺水點」水量低於平衡。當圖上有excess與deficit，表示流量不平衡，不是可行流。

積缺水量 = 流入水量 - 流出水量 + 供需水量

k vertex-disjoint paths
k edge-disjoint paths

給定k組起點與終點，找齊k條路徑，點（邊）皆相異；除了起點與終點。可能找不到。

flow問題，源點與匯點不必對應，P問題。

此問題，起點與終點必須對應，NP-complete問題。

差別在於交叉路徑。flow問題，運用溯洄沖減，交叉路徑總是變成不交叉路徑。此問題則不然。

UVa 11301

k vertex-disjoint s-t paths
k edge-disjoint s-t paths

給定一組起點與終點，找出k條路徑，點（邊）皆相異；除了起點與終點。起點都是同一點、終點都是同一點，無所謂對不對應。可能找不到。

解法是maximum s-t flow。

UVa 10806 ICPC 4259 4271

進階版本，這k條路徑的權重總和必須最小。

解法是Minimum cost maximum s-t flow。

UVa 11823 1236 ICPC 3570

multi-commodity flow

指定多組供點、需點，必須對應。

流量是實數，P問題。流量是整數，NP-complete問題，大家改為研究速度飛快的近似演算法。