closure

「閉包」。導出子圖，沒有聯外邊。可能有許多個。

minimum closure / maximum closure

「最小閉包」。點數最少的閉包，即是空圖，缺乏討論意義。

「最大閉包」。點數最多的閉包，即是原圖，缺乏討論意義。

無向圖的情況下，閉包是連通分量，缺乏討論意義。

有向圖的情況下，收縮強連通分量，得到DAG，容易找閉包。

maximum weight closure

「最大權閉包」。一張圖上，點有權重、邊無權重，點的權重總和最大的閉包。只有唯一一個。

無向圖演算法：權重最大的連通分量。

有向圖演算法：重新打造一張圖，求最小源匯割。我不知道為什麼這樣做，真是不好意思。

新增超級源點、超級匯點。源點連向所有正點，容量是正點權重；所有負點連向匯點，容量是負點權重變號；原圖的邊，容量是無限大。

最小源匯割不會包含容量無限大的邊。也就是說，源點側到匯點側，沒有容量無限大的邊、沒有原圖的邊。源點側沒有連外邊。源點側是閉包。源點側去掉源點即是最大權閉包。

// 原圖 const int V = 10; bool adj[V][V]; // adjacency matrix int v[V]; // 點權重 // 新圖 typedef int Graph[V+2][V+2]; // adjacency matrix Graph C, F, R; // 容量、流量、剩餘容量 void maximum_weight_closure() { /* 建立新圖 */ memset(C, 0, sizeof(C)); int s = V, t = V+1; // 設定源點s與匯點t for (int i=0; i<V; ++i) // 處理點 if (v[i] > 0) C[s][i] = v[i]; // add_edge(s, i, v[i]); else /* if (v[i] < 0) */ C[i][t] = -v[i]; // add_edge(i, t, -v[i]); for (int i=0; i<V; ++i) // 處理邊 for (int j=0; j<V; ++j) if (adj[i][j]) C[i][j] = INF; // add_edge(i, j, INF); /* 計算最大流、最小割 */ bool s_side[V+2]; maximum_flow(s, t, V+2, C, s_side); /* 計算maximum closure */ int weight = 0; for (int i=0; i<V; ++i) if (s_side[i]) { cout << i << "點屬於maximum closure"; weight += v[i]; } cout << "maximum closure的權重是" << weight; }

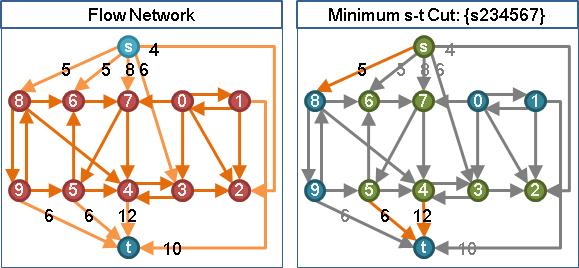
separator（separating set）（cut-set）

「分隔」、「分隔集」。細分為點和邊兩種版本：

點集合，將連通圖分離成兩個以上連通分量。

邊集合，將連通圖分離成兩個以上連通分量。

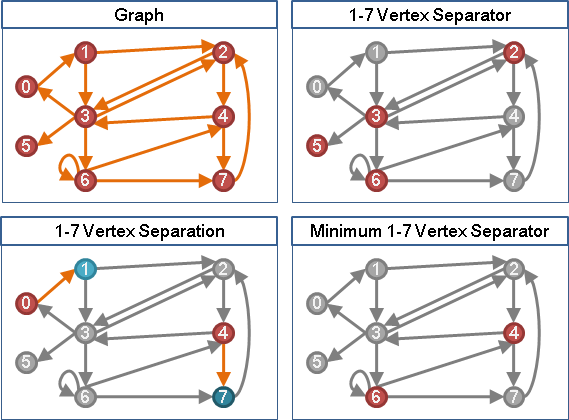
minimum separator（minimum separating set）

「最小分隔」。細分為點和邊兩種版本：

一張圖上點數最少的點分隔。可能有許多個。

一張圖上邊數最少的邊分隔。可能有許多個。

ICPC 4322 3811

(a,b)-separator

「ab分隔」。細分為點和邊兩種版本：

斷開a點到b點，使之不連通的點集合。

斷開a點到b點，使之不連通的邊集合。

事先指定兩點ab。ab不相同、不相鄰才有討論意義。

connectivity

「連通度」。細分為點和邊兩種版本：

欲讓圖不連通，至少需要拿掉的點數。

欲讓圖不連通，至少需要拿掉的邊數。

其點數、邊數，即是最小點分隔、最小邊分隔。

換句話說，一張圖上隨意拿掉「vertex connectivity減一」個點，一定還是連通的。

κ(G) ≤ λ(G) ≤ minv∈G δ(v)。點連通度小於等於邊連通度小於等於最小的度數。

Menger's theorem

「ab點互斥路徑（點不重複、端點ab除外）的數量最大值」＝「ab點分隔的點數最小值」。

「ab邊互斥路徑（邊不重複）的數量最大值」＝「ab邊分隔的邊數最小值」。

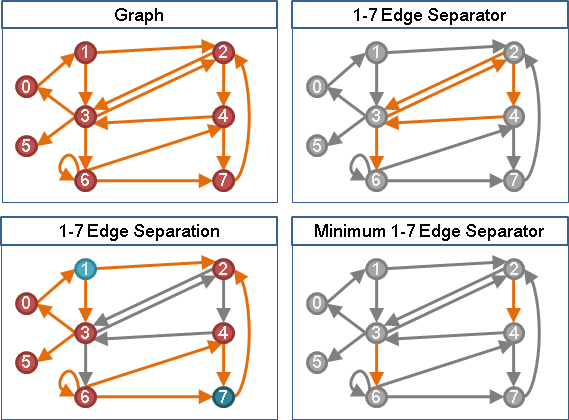
邊連通度演算法（max-flow min-cut theorem）

點容量為一：最大st流＝最小st割＝最大st互斥路徑＝最小st分隔
邊容量為一：最大st流＝最小st割＝最大st互斥路徑＝最小st分隔

窮舉所有點對，分別求最小分隔的大小，取最小值即得。

無向圖O(VE)。Stoer–Wagner algorithm。

有向圖O(VEVlogV)。Hao–Orlin algorithm。【尚待確認】

https://www.cse.msu.edu/~cse835/Papers/Graph_connectivity_revised.pdf
https://www.zhihu.com/question/265186138/answer/290977527
图是unweighted graph, 则可以先找k-certificate然后再用SW算法. 可以O(m)时间把边
的个数变成O(kn)个. 所以k很小的话速度还蛮快的.

邊連通度演算法（dominating set）

《Determining edge connectivity in O(mn)》

無向圖O(VE)或者O(λV²)。Matula's algorithm。

《Finding the edge connectivity of directed graphs》

有向圖O(VE)或者O(λ²V²)。Mansour–Schieber algorithm。

邊連通度演算法（matroid intersection）

《A matroid approach to finding edge connectivity and packing arborescences》

無向圖O(E + λ²VlogV)。有向圖O(λElogV)。Gabow's algorithm。

邊連通度演算法（local search）

《Computing and testing small connectivity in near-linear time and queries via fast local cut algorithms》

《An Experimental Study of Algorithms for Computing the Edge Connectivity of a Directed Graph》

無向圖Õ(λ²E)。有向圖Õ(λ²E)。近似演算法。

partition

strength

強壯程度。分割之間的邊數量、分割數量（減一），兩者比值的最大值。

https://en.wikipedia.org/wiki/Strength_of_a_graph

toughness

堅韌程度。刪除tk點無法得到k個連通分量。

https://en.wikipedia.org/wiki/Graph_toughness

用途

無向圖或有向圖，指定兩側點數，求出其中一個最大割。

近似演算法，讓答案盡量準確。

演算法

隨機創造一個割，逐步改成最大割。不斷對調異側兩點，盡量讓割權重變大，直到無法變大。

用途

無向圖，求出其中一個最大割。

近似演算法，讓答案盡量準確。

maximum cut

0.878 max cut
https://zhuanlan.zhihu.com/p/69126787