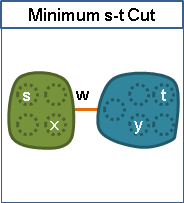
minimum cut tree（Gomory–Hu tree）

「最小割樹」。樹上任意兩點，作為s點、t點。兩點連成路徑，找到瓶頸（權重最小的邊）。瓶頸的兩側，即是s側、t側。瓶頸的權重，即是minimum s-t cut的權重。

一張無向圖的最小割樹，可能有許多棵。一張有向圖的最小割樹，至今仍未被發現。

最小生成樹：任意兩點之間的路徑，最寬的邊盡量窄。
最小割樹：任意兩點之間的所有通道，最寬的切面盡量窄。

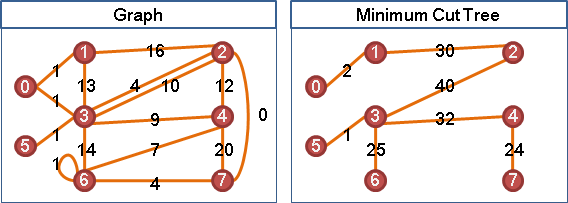
UVa 11603 10816 ICPC 4848

數學性質：submodularity

兩個集合、交集、聯集，四者之間的不等式。

當圖上無負邊，任意兩個割，其權重都符合這個不等式。

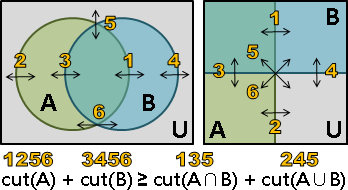
數學性質：聯集交集

最小st割、最小xy割，S∪X與T∩Y形成新的割。

當交集不是空集合，新的割可能是：另一個最小st割、另一個最小xy割、權重更小或一樣的其他割、權重不明的其他割。

根據stxy四個點所在位置，可以鑑定結果是哪幾種。

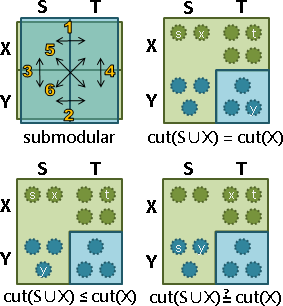
一、令cut(S)是最小st割。令cut(X)是最小xy割。
　　cut(S) + cut(X) ≥ cut(S∩X) + cut(S∪X)。
二、討論cut(S∩X)：
　甲、假設cut(S∩X)不含s點、不含t點。
　　　此時歸納不出任何結論。
　乙、假設cut(S∩X)含有s點、不含t點，是個st割。
　　　因為cut(S∩X)是st割，又知道cut(S)是最小st割，所以
　　　cut(S∩X) ≥ cut(S)。
　　　然後併入步驟一的結論，輕鬆得到
　　　cut(S∪X) ≤ cut(X)。
三、討論cut(S∪X)：
　甲、假設cut(S∪X)含有x點、不含y點，是個xy割。
　　　以最小xy割cut(X)為基準，根據叛離性質，
　　　cut(S∪X)的權重只會變大（或不變），所以
　　　cut(S∪X) ≥ cut(X)。
　　　然後併入步驟二乙的結論，輕鬆得到
　　　cut(S∪X) = cut(X)。
　　　證得cut(S∪X)與cut(X)都是最小xy割。
　乙、假設cut(S∪X)含有x點也含有y點，不是個xy割。
　　　此時無法套用叛離性質。
　　　使用步驟二乙的結論
　　　cut(S∪X) ≤ cut(X)。
　　　證得cut(S∪X)是比cut(X)權重更小（或一樣）的其他割。

順帶一提，
步驟二，改為假設cut(S∩X)是xy割。
步驟三，改成st割。
最後證得cut(S∪X)與cut(S)的關係。

附帶一提，無向圖上，一個割的兩側，對調也無妨。
cut(S∪X) = cut(T∩Y)。

數學性質：瓶頸

最小割樹，任兩點路徑瓶頸，形成最小源匯割。

已知一個最小st割。隨意取兩個點，x點與y點。

一、兩點都在s側（或者兩點都在t側）：

根據交集聯集性質，最小xy割不只一個。某個最小xy割的某一側，可以完全包含t側。收縮t側，不影響某些最小xy割！

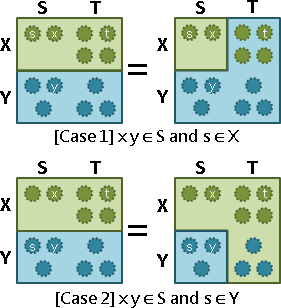
二、x點在s側、y點在t側（或者反過來）：

根據基準性質，「最小xy割的權重」小於等於「最小st割的權重」。

用途

無向圖，求得其中一棵最小割樹。

限制：無負邊。

演算法

divide-and-conquer method。求V-1次最小源匯割。

divide：
隨便求一個minimum s-t cut，得到s側、t側。
注意到s點和t點必須是圖上原本的點，而不是收縮之後的點。

conquer：
此圖收縮t側（得t'點），遞迴求解，得到s側的minimum cut tree。
此圖收縮s側（得s'點），遞迴求解，得到t側的minimum cut tree。

combine：
新增邊s't'，權重設定為minimum s-t cut的權重。
所有新增的邊，最後拼在一起，構成一棵minimum cut tree。

如果原圖已經有一部分是樹，此部分顯然就是最小割樹，不必再逐次計算最小st割。

時間複雜度

下列三項總和，主要取決於第一項：

一、求V-1次最小源匯割。

二、收縮點，O(V²)。

三、新增邊，共V-1條邊，O(V)。

查詢最小源匯割

最小割樹，隨便選定一個根，變成有根樹。仿照lowest common ancestor演算法，計算源匯路徑的瓶頸（最小值），得到最小源匯割。

例如建立表格，得到所有兩點之間的最小源匯割，時間複雜度與空間複雜度都是O(V²)。

例如jump pointer algorithm，建立二的次方祖先表格，即時查詢路徑最小值。建立O(VlogV)、查詢O(logV)。

const int V = 10; int R[V][V]; // residual graph // 重新初始化剩餘容量 void residual_graph() { for (int i=0; i<V; i++) for (int j=i+1; j<V; j++) { int r = (R[i][j] + R[j][i]) / 2; R[i][j] = R[j][i] = r; } } int maximum_flow(int s, int t) { ...... } bool visit[V]; // DFS visit // 尋找s側 void DFS(int i) { if (visit[i]) return; visit[i] = true; for (int i=0; i<V; ++i) if (R[i][j] > 0) DFS(j); } vector<pair<int,int>> tree[V]; // minimum cut tree int cut[V]; // minimum cut void minimum_cut_tree(int L, int R) { if (L >= R) return; // 最小st割 // 隨便抓兩點，此處抓L和R。 int s = cut[L]; int t = cut[R]; residual_graph(); int f = maximum_flow(s, t); // 新增邊st tree[s].push_back({t, f}); tree[t].push_back({s, f}); // s側 memset(visit, false, sizeof(visit)); DFS(s); // 重新分成兩側 int M = L; for (int i=L; i<=R; i++) if (visit[cut[i]]) swap(cut[i], cut[M++]); // 兩側分別遞迴求解，如此就不必收縮。 minimum_cut_tree(L, M-1); minimum_cut_tree(M, R); } int ans[V][V]; bool visit[V]; void DFS(int s, int i, int minw) { if (visit[i]) return; visit[i] = true; ans[s][i] = minw; for (auto [j, w]: tree[i]) DFS(s, j, min(minw, w)); } void table() { for (int i=0; i<V; ++i) { memset(visit, false, sizeof(visit)); DFS(i, i, INT_MAX); } } int adj[V][V]; // adjacency matrix void gomory_hu() { memcpy(R, adj, sizeof(adj)); for (int i=0; i<V; ++i) cut[i] = i; minimum_cut_tree(0, V-1); table(); }

UVa 11603

用途

無向圖，求得其中一棵最小割樹。

限制：無負邊。

演算法

incremental method。求V-1次最小源匯割。

一、初始化最小割樹：
　　第零點是中心，第一點到第V-1點皆連向第零點。
二、依序處理第一點到第V-1點：
　甲、當前點s，只有連向點t。
　　　邊st的權重設定為最小st割的權重。
　乙、屬於s側的點x，全部改為連往s點。
　　　邊xs保持原本設定的權重。

【待補程式碼】

equivalent flow tree

簡易版的最小割樹。此樹只能求得最小st割的權重，但是不能求出最小st割。

一、初始化最小割樹：
　　第零點是中心，第一點到第V-1點皆連向第零點。
二、依序處理第一點到第V-1點：
　甲、當前點s，只有連向點t。
　　　邊st的權重設定為最小st割的權重。
　乙、屬於s側、並且尚未處理的點，全部改為連往s點。

int adj[9][9]; // adjacency matrix int p[9]; // equivalent flow tree int c[9][9]; // 所有兩點之間最小st割的權重 void gusfield() { memset(p, 0, sizeof(p)); // star graph memset(c, 0x7f, sizeof(c)); // 預設為無限大 for (int i=1; i<9; ++i) { // 找出最小i p[i]割，並找出i側有哪些點。 bool i_side[9]; // BFS visit record int f = maximum_flow(i, p[i], i_side); // i點以後的點（尚未處理的點）， // 屬於i側、但是連往p[i]點的，就改連到i點。 for (int j=i+1; j<9; ++j) if (i_side[j] && p[j] == p[i]) p[j] = i; // 順便計算各點與i的最小st割的權重。 c[i][p[i]] = c[p[i]][i] = f; for (int j=0; j<i; ++j) c[i][j] = c[j][i] = min(f, c[p[i]][j]); } // 最後把對角線設回為零 for (int i=0; i<9; ++i) c[i][i] = 0; }

UVa 11594

Steiner cut

一張圖，指定一些點，找到一個割，將這些點分為兩側。

minimum Steiner cut

權重最小的Steiner cut，可能有許多個。

演算法是取這些點作為minimum cut tree。

minimum Steiner tree是NP-complete問題，minimum Steiner cut是P問題。