convex hull
3D convex hull
3D convex hull:
Graham's scan
3D convex hull:
gift wrapping algorithm
3D convex hull:
monotone DAG
3D convex hull:
incremental method
3D convex hull:
divide-and-conquer method
3D convex hull:
quick hull algorithm

3D convex hull

3D convex hull

三維凸包的表面，由數個凸多邊形拼成。

為了方便儲存，凸多邊形剖分成數個三角形。

為了方便儲存，多點共面剖分成數個三角形。

三維凸包的表面，由數個三角形拼成。

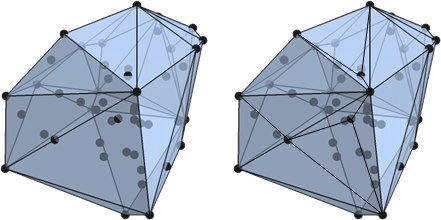
p = {{5,4,8},{1,8,6},{6,6,4},{9,6,4},{7,9,7},{6,9,9},{8,0,8},{1,5,4},{1,1,5},{6,6,3},{8,6,7},{0,1,6},{9,7,10},{7,6,3},{6,2,7},{10,4,4},{5,8,2},{8,3,2},{2,6,3},{0,0,1},{7,3,3},{6,9,8},{2,8,1},{10,6,10},{5,8,10},{8,2,4},{5,7,6},{6,7,2},{1,10,1},{0,4,5},{1,3,2},{8,1,0},{4,10,2},{1,9,0},{6,3,5},{9,1,3},{8,10,1},{9,6,8},{6,2,3},{10,0,2},{8,1,10},{10,2,4},{9,0,10},{2,9,6},{10,5,10},{4,0,5},{2,3,8},{3,8,4},{3,3,10},{4,5,1}};

我們習慣以逆時針順序記錄三角形的三個頂點（三角形的三條邊變成有向邊）。這麼做的好處是，三角形依序取兩條邊計算叉積，就得到朝外的法向量。

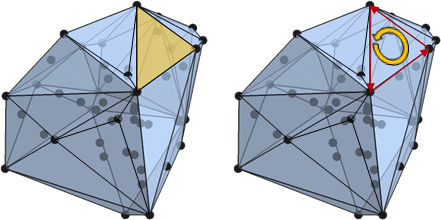
facet

高維度空間的物體，一塊平坦表面稱作「刻面」，就好像被刻了一刀。鑽石就是刻面的極致工藝。

為了方便儲存，刻面從凸多邊形變成三角形。

3D convex hull:
Graham's scan

三維凸包的繞行順序是什麼？

二維凸包的頂點，以時針順序繞行一圈。三維凸包的頂點，至今仍未發現適當的繞行順序。三維的 Graham's scan 至今仍是懸案。

3D convex hull:
gift wrapping algorithm

演算法

找到第一個凸包刻面：座標最低的三個點。

以邊為軸，旋轉的掃描面，尋找最外圍的點，包覆成新刻面。

當凸包多點共面，在掃描面上尋找二維凸包、尋找三角剖分。

時間複雜度 O(FNlogN) ， F 是凸包刻面數量。多面體最多有 O(N) 個面，時間複雜度可寫作 O(N²logN) 。

3D convex hull:
monotone DAG

monotone chain 可以推廣成 monotone DAG 嗎？

等你發表論文。

3D convex hull:
incremental method

演算法

逐次增加一點，更新刻面。

運用刻面法向量，判斷刻面屬於凸面、凹面、切面。

運用刻面有向邊，找到凹切分際。

保留凸面與切面，移除凹面，添加當前輸入點到凹切分際的新刻面。如此便完成了新凸包。

預先按照 XYZ 座標排序所有點（平移的掃描面），就能保證當前輸入點都在凸包外部，就能保留多點共面的三角剖分。

時間複雜度 O(N²) 。加速為 O(NlogN) 至今仍是懸案。

  1. // 凸包的頂點
  2. struct Point {float x, y, z;} p[10];
  4. Point operator-(Point a, Point b)
  5. {
  6. return (Point){a.x - b.x, a.y - b.y, a.z - b.z};
  7. }
  9. double dot(Point a, Point b)
  10. {
  11. return a.x * b.x + a.y * b.y + a.z * b.z;
  12. }
  14. Point cross(Point a, Point b)
  15. {
  16. return (Point){a.y * b.z - b.y * a.z,
  17. a.z * b.x - b.z * a.x,
  18. a.x * b.y - b.x * a.y};
  19. }
  21. bool zero(Point a)
  22. {
  23. return a.x == 0 && a.y == 0 && a.z == 0;
  24. }
  26. bool cmp(Point a, Point b)
  27. {
  28. if (a.x != b.x) return a.x < b.x;
  29. if (a.y != b.y) return a.y < b.y;
  30. return a.z < b.z;
  31. }
  33. // 凸包的刻面
  34. // 一個刻面為三個頂點（索引值），逆時針順序為向外。
  35. struct Facet {int a, b, c;};
  37. Point normal(Facet f)
  38. {
  39. return cross(p[f.b] - p[f.a], p[f.c] - p[f.a]);
  40. }
  42. // 凸包的刻面的有向邊
  43. // 一條有向邊為兩個頂點（索引值）
  44. int vis[10][10];
  46. void convex_hull()
  47. {
  48. // 預先排序
  49. sort(p, p+10, cmp);
  51. /* 必須弄出一個四面體。 */
  53. // 四面體頂點（索引值）
  54. int v0, v1, v2, v3;
  56. // 指定第一點
  57. v0 = 0;
  59. // 令前兩點不共點
  60. int i = 0;
  61. for (++i; i<10; ++i)
  62. if (!zero(p[i] - p[v0]))
  63. {
  64. v1 = i;
  65. break;
  66. }
  67. if (i == 10) return; // 通通共點
  69. // 令前三點不共線
  70. for (++i; i<10; ++i)
  71. if (!zero(cross(p[v1] - p[v0], p[i] - p[v0])))
  72. {
  73. v2 = i;
  74. break;
  75. }
  76. if (i == 10) return; // 通通共線
  78. // 令前四點不共面
  79. Point n = cross(p[v1] - p[v0], p[v2] - p[v0]);
  80. float d = 0;
  81. for (++i; i<10; ++i)
  82. if ((d = dot(n, p[i] - p[v0])) != 0)
  83. {
  84. v3 = i;
  85. break;
  86. }
  87. if (i == 10) return; // 通通共面
  89. /* 開始建立凸包 */
  91. // 前四點形成的凸包
  92. vector<Facet> cur;
  93. if (d > 0)
  94. {
  95. cur.push_back((Facet){v1,v0,v2});
  96. cur.push_back((Facet){v0,v1,v3});
  97. cur.push_back((Facet){v1,v2,v3});
  98. cur.push_back((Facet){v2,v0,v3});
  99. }
  100. else
  101. {
  102. cur.push_back((Facet){v0,v1,v2});
  103. cur.push_back((Facet){v1,v0,v3});
  104. cur.push_back((Facet){v2,v1,v3});
  105. cur.push_back((Facet){v0,v2,v3});
  106. }
  108. // 處理其餘點
  109. for (int i=0; i<10; ++i)
  110. {
  111. if (i == v0 || i == v1 || i == v2 || i == v3)
  112. continue;
  114. vector<Facet> next;
  116. // 保留凸面與切面、移除凹面
  117. for (int j=0; j<cur.size(); ++j)
  118. {
  119. Facet& f = cur[j];
  121. // 保留凸面與切面
  122. double d = dot(p[f.a] - p[i], normal(f));
  123. if (d >= 0) next.push_back(f);
  125. // 刻面有向邊，記錄凸面、凹面、切面。
  126. int side = 0; // 切面
  127. if (d > 0) side = +1; // 凸面
  128. if (d < 0) side = -1; // 凹面
  129. vis[f.a][f.b] = side;
  130. vis[f.b][f.c] = side;
  131. vis[f.c][f.a] = side;
  132. }
  134. // 添加當前輸入點到凹凸分際的新刻面
  135. for (int j=0; j<cur.size(); ++j)
  136. {
  137. Facet& f = cur[j];
  138. int a = f.a, b = f.b, c = f.c;
  140. // 找到凹面，分別觀察三條邊，判斷是否為凹凸分際。
  141. if (vis[a][b] < 0 && vis[a][b] != vis[b][a])
  142. next.push_back((Facet){a, b, i});
  144. if (vis[b][c] < 0 && vis[b][c] != vis[c][b])
  145. next.push_back((Facet){b, c, i});
  147. if (vis[c][a] < 0 && vis[c][a] != vis[a][c])
  148. next.push_back((Facet){c, a, i});
  149. }
  151. cur = next;
  152. }
  153. }

UVa 11769 12513 ICPC 5090 4795

3D convex hull:
divide-and-conquer method

演算法

所有點分成左右兩堆，分別求凸包。合併兩個凸包，用滾動的。筷子串起兩個凸包，放在地上滾，以筷子為軸轉一圈。

時間複雜度 O(NlogN) 。

3D convex hull:
quick hull algorithm

演算法

時間複雜度 O(N²) 。實務上最快的演算法。