coloring
coloring
vertex coloring
vertex coloring
「點著色」。一張圖每個點塗上顏色,鄰點不同色。
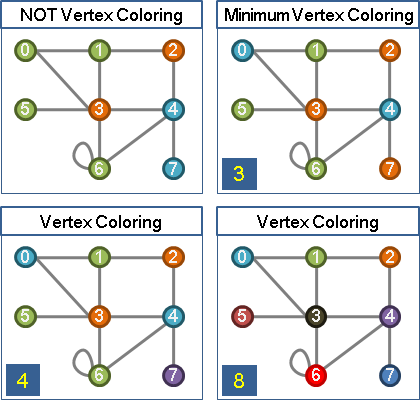
minimum vertex coloring / chromatic number
「最小點著色」是顏色數目最少的點著色,可能有許多種。「最小著色數」是最小點著色的顏色數目。NP-complete。
原圖的minimum vertex coloring,等於補圖的minimum clique cover。
k-vertex coloring
「k點著色」。使用k種顏色完成點著色。NP-complete。
特殊圖可推理出最小著色數的上限(保證可著色數的下限)。
G沒有點和邊:χ(G) = 0 G沒有邊:χ(G) ≤ 1 G為二分圖(bipartite graph):χ(G) ≤ 2 G為平面圖(planar graph):χ(G) ≤ 4(四色定理) G為完全圖(complete graph):χ(G) = V G的每個點的連接邊數相同(k-regular):χ(G) ≤ k + 1 G的每個點的連接邊數不同(non-regular),也就是一般的圖:χ(G) ≤ Δ(G) χ(G):一張圖G的最小著色數。 Δ(G):一張圖G的最大degree。
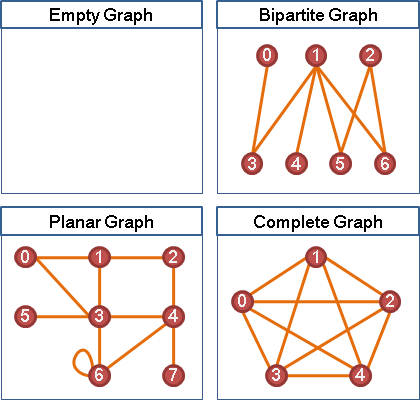
UVa 10661 10004 10052
greedy vertex coloring / Grundy chromatic number
「貪心點著色」是採用貪心法而得到的點著色,可能有許多種。「Grundy著色數」是貪心點著色的顏色數目。不控制著色數。
最小點著色、k點著色,都是NP-complete問題,沒有快速的演算法。於是有些人轉為討論貪心點著色,設計快速的演算法。
演算法:無向圖點著色(Welsh–Powell algorithm)
貪心點著色。圖上每個點,依照邊數由大到小排序,依序塗色。針對一個點,依序嘗試各種顏色,直到不牴觸已塗色的點。
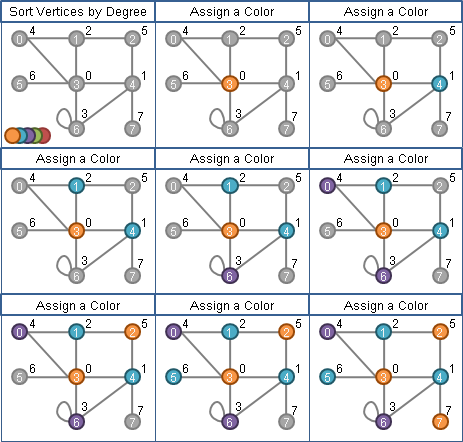
每個點的邊數是0到V-1(不考慮多重的邊、不考慮自己連向自己的邊),排序可以採用counting sort,時間複雜度O(V)。
時間複雜度等於一次graph traversal的時間。圖的資料結構為adjacency matrix是O(V²),圖的資料結構為adjacency lists是O(V+E)。
演算法:二分圖點著色
graph traversal可以判斷一張圖是否為二分圖。
順便判斷二著色。順便找出其中一種最小點著色。
演算法:平面圖點著色(four color theorem)
一張真實地圖,每塊區域塗上顏色,相鄰區域必須是相異顏色。地圖可以化作平面圖:區域是點,相鄰區域是邊。
平面圖一定可以四著色(四色定理),P問題,有著O(N²)演算法。平面圖不一定可以三著色,NP-complete問題。
四色定理的證明方式,是把所有的圖精簡成幾種基本款式,逐一驗證是否能四著色,以電腦窮舉所有著色可能性。1976年基本款式共一千多種。1997年基本款式降到六百多種,同時發明了O(N²)四著色演算法(不保證著色數最小):
有些數學家認為,電腦窮舉不是一個嚴謹的、具有數學意義的證明方式。因此這個問題現今仍有人在持續研究。
延伸閱讀:four color theorem
下面提供一些個人想法,睡不著時加減想的,應該有誤:
甲、零個點、一個點、兩個點、三個點、四個點的圖,每個點分別塗一種顏色也不會超過四種顏色,所以應該不太需要證明了。
乙、點著色的問題,圖上的邊越多,限制就越多。完全圖(complete graph)的邊是最多的,所以只要完全圖可以解決,那麼只要從完全圖上刪掉幾條邊,其他邊比較少的圖也都可以解決了。因此,這裡我們考慮一下四個點的完全圖。
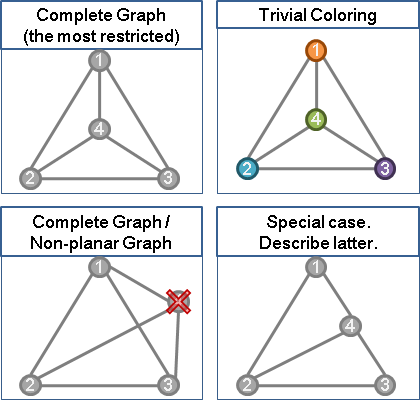
丙、由於點的編號順序是無所謂的,不失一般性,這裡我們規定前三點是最外圍的點,而之後的點皆會落在前三點所構成的範圍裡面。四個點一共將整個範圍切成四塊區域。(有一個特例是點剛好在邊上,留待最後討論。)
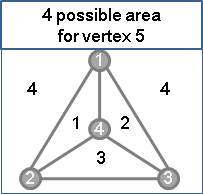
丁、第五點會落在這四塊區域的其中一塊。當然依照我們的順序規定,第五點是不可能落在第四塊區域的。若是第五點落在第一塊區域,那麼就將第五點塗上在他外邊對頂的那個點的顏色。其他區域也是類似的。
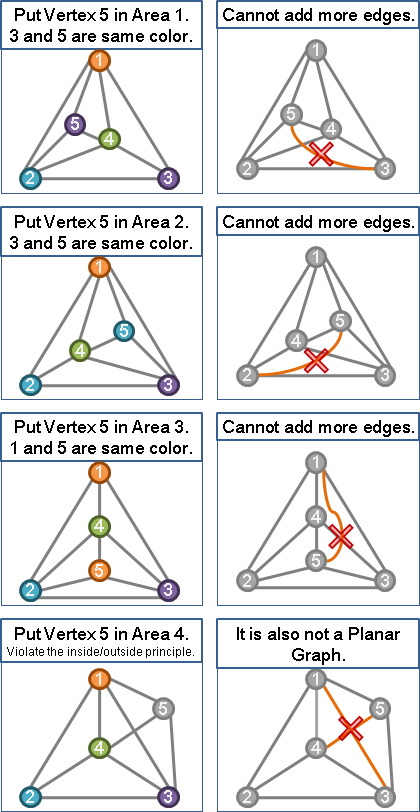
戊、決定第五點後,以divide-and-conquer method的觀點來看,構成了一個子問題。其他的區域也還是可以再放入點。放好所有點之後,只要刪除了其中的邊,就可以做出任意一種平面圖了。
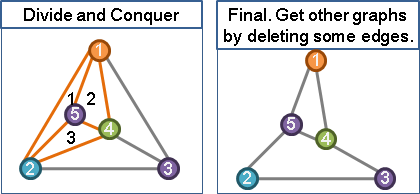
己、之前有個點在邊上的特例還沒解決。如果把點放在邊上面,可以歸類成三種情形:甲、放在最外圍的邊,乙、放在裡面的邊,但是邊的兩邊區域能容忍的顏色不相同,丙、放在裡面的邊,邊的兩邊能容忍的顏色相同。其中甲和丙都是合法操作,而乙則是不合法操作,可由別的方式來做出一樣的圖。
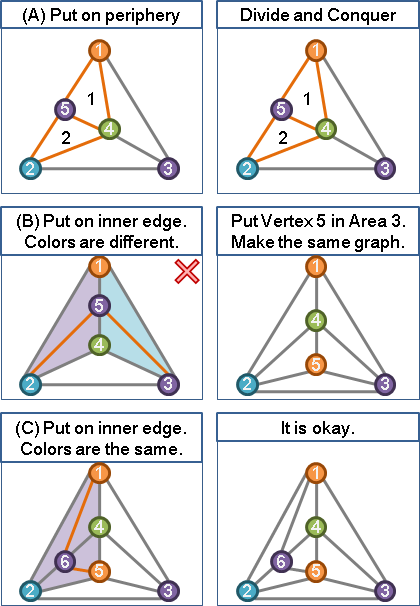
庚、最後再提供一種想法:被分割的區域們其實又形成了一個四色圖問題。
以上就是我想到的證明。理所當然是個偽證。謝謝收看。
regular graph
regular graph / factor
無向圖當中,「regular graph」是每一點都連著一樣多的邊的圖;「factor」是每一點都連著一樣多的邊的子圖。
簡而言之:每個點的邊數都一樣的圖、子圖。
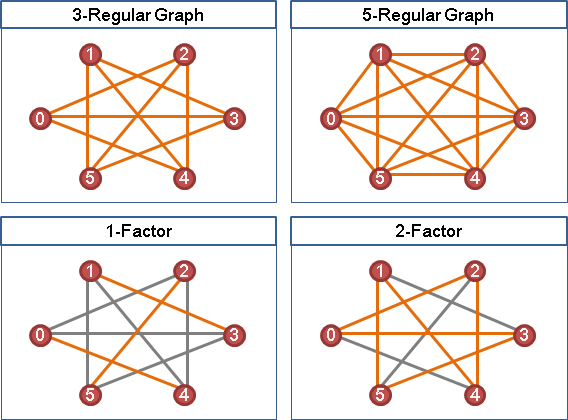
我們可以在名稱開頭冠上數字、橫槓,明確呈現邊數。例如1-regular graph是每個點都連著一條邊的圖,2-factor是每個點都連著兩條邊的子圖。
complete graph / clique
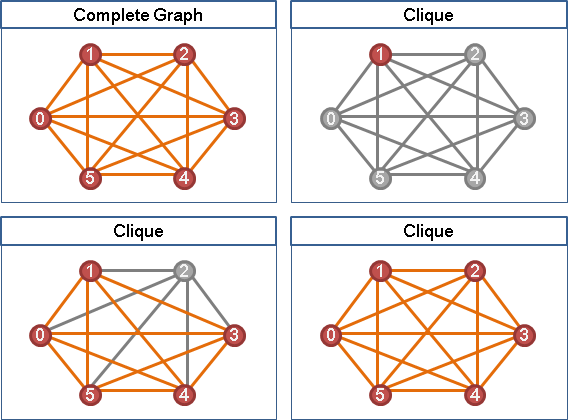
無向圖當中,「完全圖complete graph」是所有兩點之間都有一條邊的圖;「團clique」是所有兩點之間都有一條邊的子圖。
簡而言之:每個點的邊數都是V-1的圖、子圖。
Moore graph
regular graph,指定了度數degree、直徑diameter。
度數degree:一個點的邊數。
直徑diameter:兩個點的最遠距離。
critical graph🚧
symmetric graph🚧
symmetric graph
vertex-transitive graph / edge-transitive graph
orientation🚧
realization🚧
degree
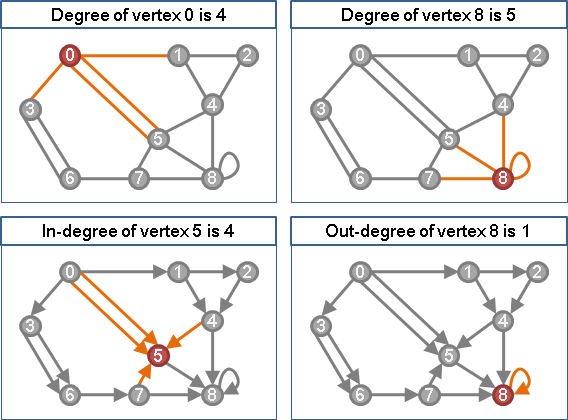
無向圖,一個點的「度degree」就是碰觸鄰邊的次數。沒有自環的情況下,「度degree」就是鄰邊數量。
有向圖,進一步細分為「入度in-degree」與「出度out-degree」,分別是指入邊數量、出邊數量。
「度」可以呈現一個點的聯繫強度。
handshaking lemma
每條邊有兩個端點,有始有終。
無向圖,整張圖的度數總和=邊數兩倍。
有向圖,整張圖的入度總和=出度總和=邊數。
UVa 12035
degree sequence
graph realization
無向圖:給定各點degree求原圖。
有向圖:給定各點in-degree與out-degree求原圖。
無向圖演算法(Erdős–Gallai theorem)
小遊戲:http://armorgames.com/play/5900/king-of-bridges
小遊戲:http://www.agame.com/game/connectors.html
求得其中一種可能性,時間複雜度O(V²)。
UVa 10720 11414
無向圖演算法(Havel–Hakimi algorithm)
度數按照大到小排序
d₁ d₂ d₃ ... is graphical
iff d₂-1 d₃-1 ... dd₁+1-1 dd₁+2 dd₁+3 dd₁+4 ... is graphical
|-------- d₁ -------|
求得其中一種可能性,時間複雜度O(V²)。
有向圖演算法(Fulkerson–Chen–Anstee theorem)
有向圖演算法(Kleitman–Wang algorithm)
求得其中一種可能性,時間複雜度O(ElogV)。
graph polynomial🚧
graph polynomial
Handbook of the Tutte Polynomial and Related Topics https://www.routledge.com/p/book/9781482240627 Fengming Dong https://scholar.google.com/citations?user=COe1tYUAAAAJ
Alon–Tarsi orientation
combinatorial nullstellensatz
Combinatorial Nullstellensatz: With Applications to Graph Colouring https://www.routledge.com/p/book/9780367686949 https://www.math.sinica.edu.tw/mathmedia/journals/4694 Tsai-Lien Wong https://math.nsysu.edu.tw/var/file/183/1183/img/44/rpttlwongwww_20210408.pdf