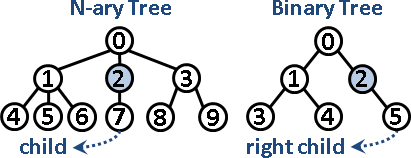
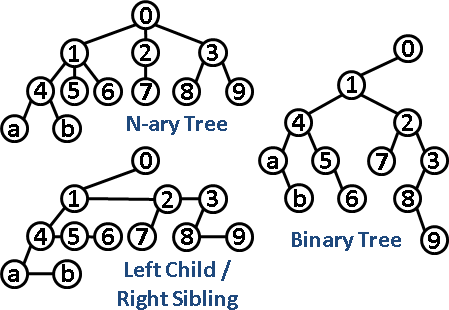
binary tree
binary tree
「二元樹」是計算機科學最重要的概念,甚至可以說:二元樹開創了計算機科學。
像是排序資料結構binary search tree、極值資料結構heap、資料壓縮Huffman tree、3D繪圖BSP tree,這一大堆稀奇古怪的術語,通通都是二元樹。二元樹的應用相當廣泛,是資工系學生必學的基礎概念。
「二元樹」與「樹」,儘管名稱相近,但是概念不相近,至於用途更是天差地遠,兩者可以分別獨立學習。二元樹:資料結構課程的二元搜尋樹章節,會順便引出二元樹的概念;樹:演算法課程的圖論章節,一開始就會介紹樹的定義。
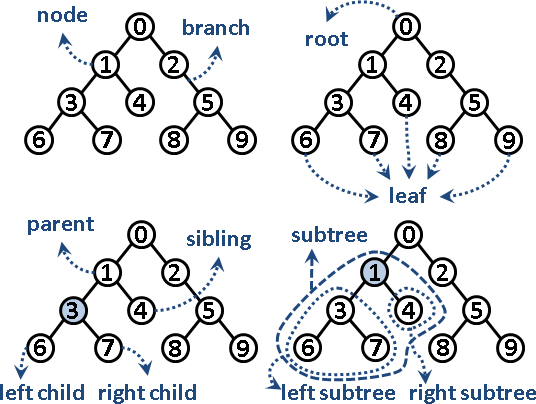
言歸正傳。「二元樹」就是分兩岔的樹,每個節點可以有左小孩和右小孩,每個節點可以有零個、一個、兩個小孩。
binary tree的形容詞
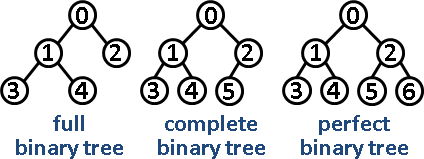
full binary tree:除了樹葉以外,每個節點都有兩個小孩。
complete binary tree:各層節點全滿,除了最後一層,最後一層節點全部靠左。
perfect binary tree:各層節點全滿。同時也是full binary tree和complete binary tree。
binary tree資料結構
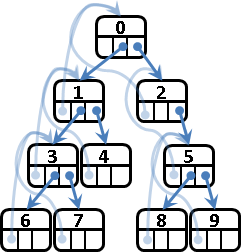
第一種方式:建立節點,以指標串接節點。
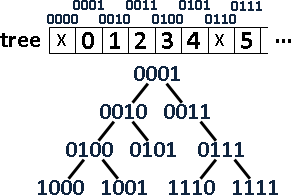
第二種方式:二進位數字一一對應到二元樹的節點。
建立一個陣列,以陣列索引值得到節點:樹根的索引值是一,索引值的兩倍是左小孩,索引值的兩倍再加一是右小孩,索引值除以二是父親。
優點是程式碼簡潔、運行速度快。缺點是浪費記憶體空間,有很多閒置空格。另一個缺點是樹的高度受限制。1024 = 2¹⁰格的陣列,樹的高度只有10,不能更高了。
UVa 122 712
binary tree traversal
二元樹的遍歷順序,理論上總共四種──但是事實上只有DFS與BFS兩種,只不過更動了節點的輸出順序。
注意樹根的位置,就能輕鬆解讀這四種序。
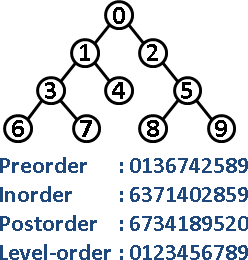
preorder traversal 前序遍歷 理論上的遍歷順序是:根、左子樹、右子樹。根排在前面。 即是depth-first search。 inorder traversal 中序遍歷 理論上的遍歷順序是:左子樹、根、右子樹。根排在中間。 實際上是採用depth-first search,只不過更動了節點的輸出順序。 postorder traversal 後序遍歷 理論上的遍歷順序是:左子樹、右子樹、根。根排在後面。 實際上是採用depth-first search,只不過更動了節點的輸出順序。 level-order traversal 層序遍歷 即是breadth-first search。
UVa 112 699
binary tree reconstruction
二元樹能得到前序、中序、後序、層序。現在反過來,前序、中序、後序、層序能得到二元樹嗎?
只有一種序,無法重建二元樹,有很多可能性。

有了兩種序,就有機會重建唯一一棵二元樹。
比方說,只有preorder和inorder,運用樹根的位置,運用divide-and-conquer Method,可以重建二元樹。
preorder之中,最左端必是樹根。inorder之中,樹根的兩側必是左子樹和右子樹。子樹也是樹,遞迴下去,求出整棵樹的架構。
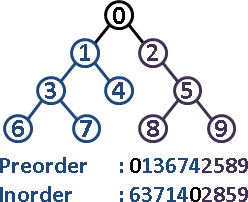
比方說,只有preorder和postorder,無法確定樹根的位置,無法重建二元樹。
那麼level-order呢?大家自己想想吧。
UVa 10701 536 548 10410 12347
Polish notation / reverse Polish notation
四則運算式子,表示成二元樹,然後列出前序、中序、後序。
前序就是波蘭表示法,又稱作prefix。中序就是原來的四則運算式子、需要括號,又稱作infix。後序就是逆波蘭表示法,又稱作postfix。
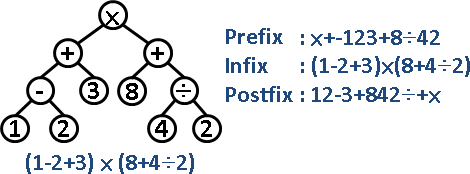
建立二元樹相當麻煩。能不能略過二元樹,直接把四則運算式子換成波蘭表示法(逆波蘭表示法)呢?當然能!運用stack即可!
四則運算式子,改成波蘭表示法(逆波蘭表示法)之後,計算過程變成由左往右計算,不必顧慮先乘除後加減、不必顧慮括號,只需要一個額外的stack作為輔助。
程式語言的四則運算式子,事實上都會被編譯器轉換成波蘭表示法(逆波蘭表示法),以利電腦計算。
UVa 372 727 11234 172 10700 10847