物理、悟理 103

前情概要

科里奧利力(科氏力)是以牛頓力學為基礎的。1835年，法國氣象學家科里奧利（Gaspard-Gustave Coriolis）提出，為了描述旋轉體系的運動，需要在運動方程中引入一個假想的力，這就是科里奧利力。引入科里奧利力之後，人們可以像處理慣性系中的運動方程一樣簡單地處理旋轉體系中的運動方程，大大簡化了旋轉體系的處理方式。由於人類生活的地球本身就是一個巨大的旋轉體系，因而科里奧利力很快在流體運動領域取得了成功的應用。
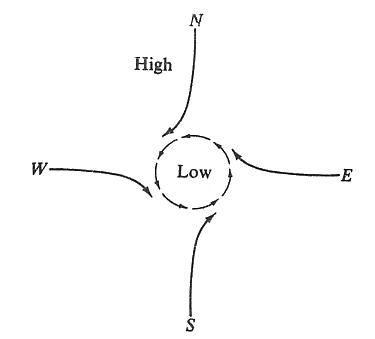
科里奧利力(科氏力)來自於物體運動所具有的慣性，在旋轉體系中進行直線運動的質點，由於慣性的作用，有沿著原有運動方向繼續運動的趨勢，但是由於體系本身是旋轉的，在經歷了一段時間的運動之後，體系中質點的位置會有所變化，而它原有的運動趨勢的方向，如果以旋轉體系的視角去觀察，就會發生一定程度的偏離。

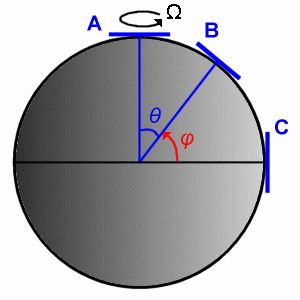
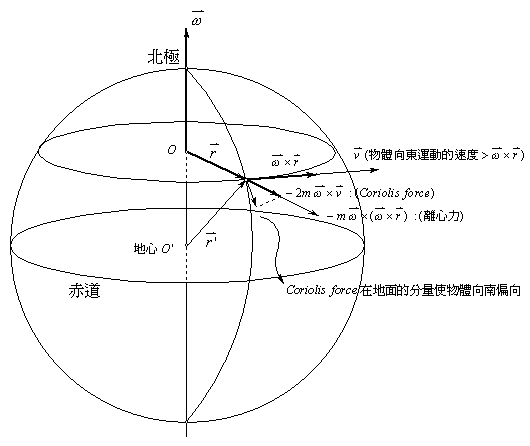
科式力公式推導 如果有個物體由北極點以直線運動，運動速率為v，而地球的自轉角速度為ω，而這物體移動時間為t，以下式子代表該物體的運動情形：
1.物體直線移動的距離：vt
2.物體在由北極上空觀察到的移動角度：ωt
綜合以上兩式子，得到該物體移動的弧長S：
=> 弧長＝移動角度 × 直線移動距離
=> S ＝ωt × vt ＝vωt^2
依照受力的直線運動公式，得出S ＝ (1/2) × a t^2，因此，兩式相等，並表示如下：
=> vωt^2＝ (1/2) × a t^2
=> a＝2vω
物體在北極上空所觀察的受力 可表示為： f＝ma＝2mvω 因為科式力是相對地球自轉的運動而假想出來的力，當另一物體由北極點以v的等速拋出時，由北極上空觀察該物體受到相反方向但相同大小的科氏力： 科式力＝－ma＝－2mvω 不同緯度，科式力的影響不同。在地球的兩極最強，赤道最弱，所以我們可以由簡單的幾何關係推導出，適用於不同緯度的科式力推倒公式，如下： F(θ)科式力＝f × cosθ， 緯度φ＝90°－θ 所以，科式力公式：F(φ)科式力＝f × sinφ＝－2mvωsinφ

相關連結:  Coriolis effect  有動畫可以模擬            資料來源:  wikipedi  科氏力