
二元一次方程式與直角坐標平面的關係
何謂方程式的解?
解的意思就是代入會滿足方程式
例如:方程式2x+3y=5的其中一個解為x=1,y=1,因為2*1+3*1=5
二元一次方程式在直角坐標平面上的圖形
因為二元一次方程式的解都是x=?,y=?,於是把x的值跟y的值用坐標來表示
例如:上面的例子中得2x+3y=5的一解為x=1,y=1,用坐標表示為(1,1),再把坐標標在坐標平面上

把方程式的解都標在坐標平面上就是方程式的圖形了
我們習慣上會用表格來記錄方程式的解

如2x+3y=5的其中五組解為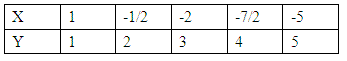
將他們畫在坐標平面上

從x=-5到x=5間找100個點後標在坐標平面上的圖形

如果把2x+3y=5的圖形畫在坐標平面上為
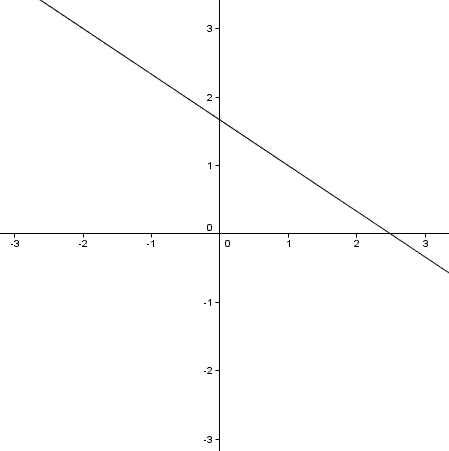
因此我們發現把二元一次方程式畫在直角坐標平面上是直線
又我們知道兩點就可以畫一條直線,所以只要找方程式的兩組解就可以畫方程式的圖形了
如何就條件來找出"直線"方程式
如果給定兩點要找方程式(因為兩點可畫出一線,又直線都可以找到與其對應的二元一次方程式)
第一種方式可以假設方程式為y=ax+b(不可以假設ax+by=c,因為三個未知數需要三個式子才能解,而兩點只有兩個式子),再把兩點代入求出a和b
例如要求過(1,1)和(-2,3)的直線方程式
首先先假設方程式為y=ax+b
再來將點代入得1=a*1+b和3=a*(-2)+b,接著解聯立就可以得出a=-2/3,b=5/3
所以過那兩點的方程式為y=(-2/3)x+5/3
接著介紹點斜式,首先介紹斜率
斜率就如同它字面的意思,即傾斜的比率
可以用上下樓梯的想法來看
越斜的意思就是越難走,即每一步要走的高度越高

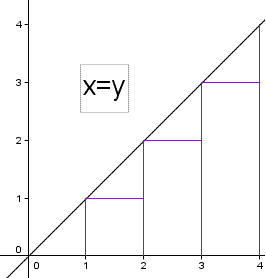
所以斜率也就是x增加1時y增加的值
當然樓梯也有向下的
當向下時斜率就是負的
我們會用那條線上任兩點的y值差除以x值差來算那條線的斜率
*注意如果x值差是用a點的x值減b點的x值則y值差也要用a點的y值去減b點的y值
而且如果過一點且斜率固定則只會有一條線滿足
假設有兩條線過那一點且方程式化簡後仍然不一樣,則他們的斜率不一樣
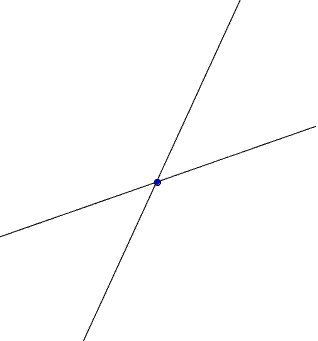
接著又發現如果把方程式寫成y=ax+b的形式,a就是斜率
假設那條線上其中兩點的坐標為(x1,ax1+b),(x2,ax2+b)
則那條線的斜率為((ax1+b)-(ax2+b))/(x1-x2),會等於a
所以也可以利用斜率來求方程式
而由斜率和點找出方程式的方式就稱為點斜式
式子為y-b=m(x-a)或者為y=m(x-a)+b其中m是斜率,(a,b)是通過的點(因為(a,b)代入滿足方程式)
像是上面那個例子
可以先算斜率
用y值差除以x值差來求,為(1-3)/(1-(-2))=-2/3
再用其中一點跟斜率來找出方程式得y=-2/3(x-1)+1或是y=-2/3(x-(-2))+3
化簡後會發現兩方程式一樣
讓各位自己試試看,在框框中輸入斜率,以及把點移到喜歡的位置
|
GeoGebra 製作 |
再來介紹截距式
x截距就是y=0代入方程式所求出的x值,y截距就是x=0代入方程式所求出的y值
而截距式就是用截距來找出方程式,式子為x/a+y/b=1其中a為x截距,b為y截距
因為當y=0代入時得x=a,x=0代入時得y=b
*注意直線的x截距為直線跟x軸的交點到y軸的距離,y截距為直線跟y軸的交點到x軸的距離
兩條線在直角坐標平面的關係
兩條線在平面上的關係只有平行、重疊、交一點、垂直其中重疊算平行的特例,垂直算交一點的特例
平行
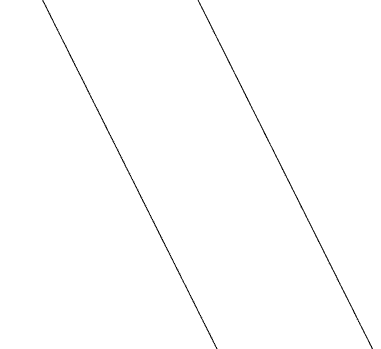
重疊
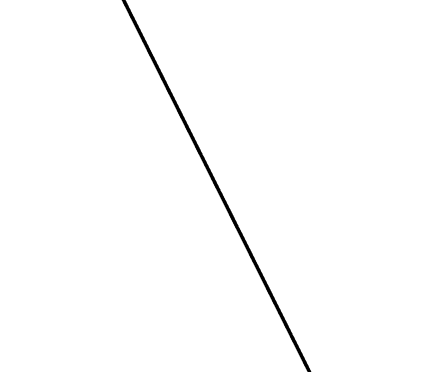
交一點
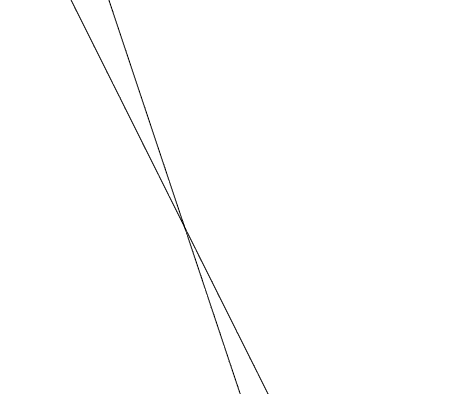
垂直
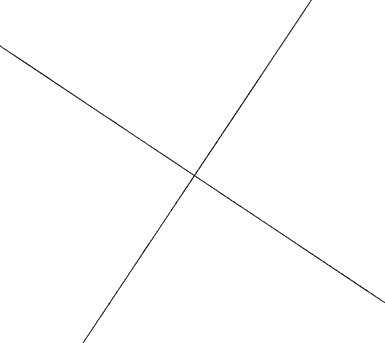
什麼時候平行呢?
當兩方程式斜率相同時,兩條線就會平行囉
如2x+3y=5和4x+6y=5,2/4=3/6

重疊就是兩個方程式其實是一樣的,就是可以利用等量公理把兩條方程式弄成一樣
如2x+3y=5和4x+6y=10,2(2x+3y)=2*5→4x+6y=10
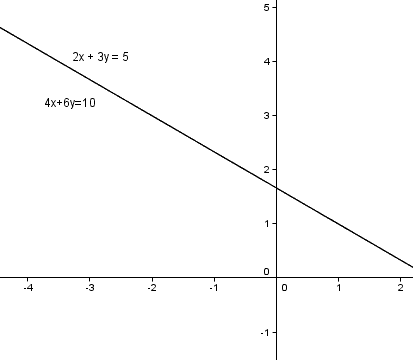
若兩條線不平行則必交一點
如2x+3y=5和2x+4y=5
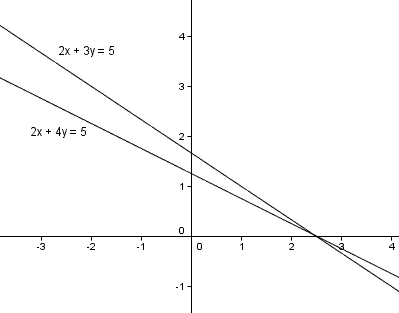
什麼時候垂直呢?
當兩方程式的斜率乘起來為-1時,兩條線就會垂直囉
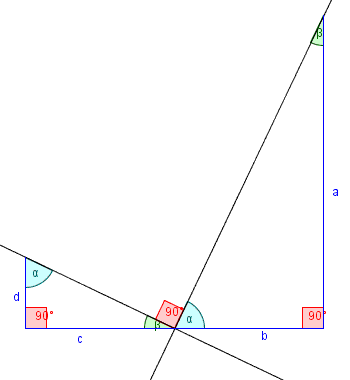
根據上圖可以發現右邊的三角形和左邊的三角形相似
又右邊這條黑線的斜率是a/b左邊那條黑線是-d/c
但是兩三角形相似,所以a/b=c/d,則兩條黑線的斜率乘起來為-1
如2x+3y=5和3x-2y=5
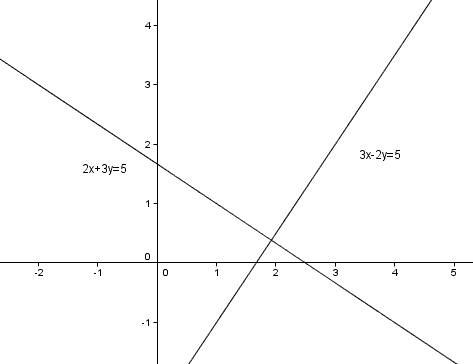
請自己試試吧
|
GeoGebra 製作 |
二元一次聯立方程式解的幾何意義
根據上面的介紹,知道可以把二元一次方程式畫在坐標平面上為一直線
那聯立方程式的話,就可以在坐標平面上畫出兩條線
又知道線所代表的意思是方程式的解
而二元一次方程式的解為滿足兩個方程式的解
也就是這解如果畫在坐標平面上會同時在兩條線上
滿足這條件的就是交點
因此二元一次聯立方程式解的幾何意義就是兩條線的交點
如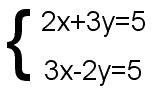
把它畫在坐標平面上
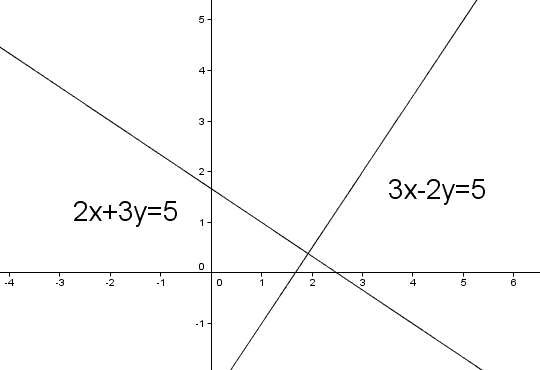
此聯立方程式的解為x=25/13,y=5/13
把它畫在坐標平面上
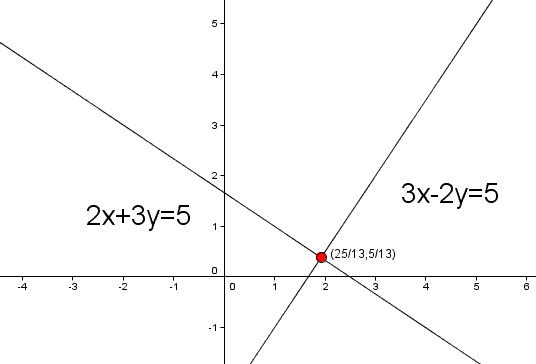
就會發現它真的會是交點