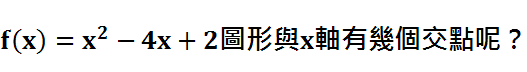
交點問題 圖形與軸交點 兩圖形交點 勘根定理 代數基本定理 平移
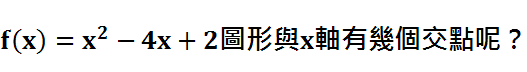
一般人直覺想法是:先畫出圖形 再數有幾個交點
交點問題看似為幾何問題 事實上可用代數層面去思考
x軸即為y=0
因此原題可完全轉換為
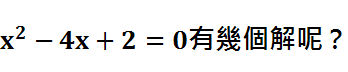
比起畫圖是不是快多了呢?
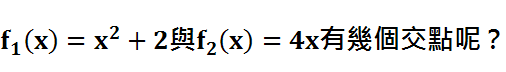
鑑於作圖的精準度 這題如果也用畫圖來看會困難多了
我們一樣可以透過轉換:
![]()
神奇的是 這就回到第一題的樣子了
實際上兩圖形交點問題可以完全轉換為圖形與x軸交點問題!
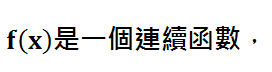
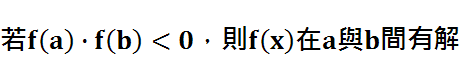
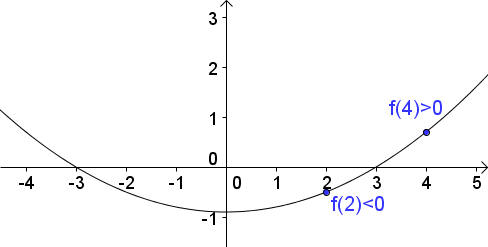
以上圖為例 f(2)<0, f(4)>0 則在 ( 2 , 4 )區間必定存在解
由定理我們只要把a跟b取很靠近 就能找到解的範圍了
動動腦:下面的敘述正確嗎?
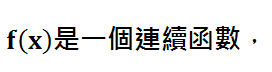
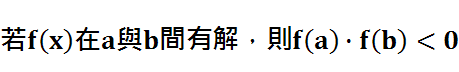
錯 以上圖為例 f(x)在( -4 , 4 )之間有解 但f(-4)>0, f(4)>0
『對於任意複係數 n次多項式至少有1複數根』
n次多項式至少有1根 用因式定理把他提出來 變成n-1次多項式至少有1根 持續使用代數基本定理 可以得到n次多項式恰有n個複數根
複數不在目前我們討論的範圍 只討論實數部分
也就是『實數n次多項式最多有n個實數解』
亦即『n次函數圖形與x軸最多有n個交點』
回想我們所學的
3次函數是不是最多2個解
2次函數是不是最多1個解
當然我們可以從原圖形找點
把點作平移 再描點形成為新圖形
但這樣太繁雜了!
舉例說明:
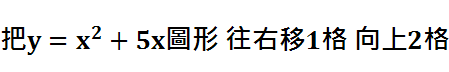
我們知道( 0 , 0 )是舊圖形點 因此( 0+1 , 0+2 )為新圖形的點
( 1 , 6 )是舊圖形點 因此( 1+1 , 6+2 )為新圖形的點
圖形平移並不會改變其形狀 也就是首項和次數都不會改變的
因此新圖的的x必須減少1 y必須減少2才能滿足原來的關係式
也就是新圖形為
![]()