函數就像是一個「機器」,它能夠將集合A裡面的每一個元素「唯一地」對應到集合B裡的一個元素。每給定一個集合A(定義域)內的元素,就能對應到集合B(對應域)內的元素,而且只能對應到一個集合B內的元素。所以函數只有可能是一對一函數,多對一函數,而不會是一對多。 通常函數用英文字f稱之,記為f:A→B。
假設A={1,2,3,4},B={1,2,3},f為A對應之B的函數,對應關係如下:
1→3,記為f(1)=3 ; 2→1,記為f(2)=1 ; 3→3,記為f(3)=3 ; 4→2,記為f(4)=2

在定義域中的任一x值畫一垂直於x軸的直線,必和函數的圖形只交於一點。若相交於兩點以上則違反了函數定義中僅有的對應規則,則不會是一個函數的圖形。
動動腦:
以下哪一個是函數?
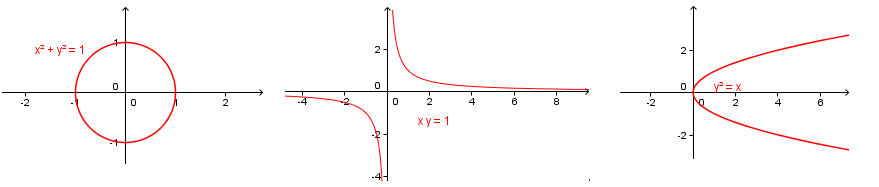
xy=1是函數圖形 (y=1/x)(反白看解答)
多項式是由變數以及數字(一般是實數或複數)經乘法及加法構法而成,屬於整式的代數式。我們都知道生活中不論物理,工程,數學,商業...等等許多領域,都是一種因為什麼而觸發什麼結果。這種因果關係,就是函數的一項重要特徵。
多項式並非描述函數的唯一方法。例如: 三角函數:y=sinx,對數:y=logx 等等.....這些函數又叫做" 非線性函數"
這些函數出現在許多電機工程、物理科學... 等等,往往描述起來過於複雜,不像多項式擁有高度的代數性質。而所有自然界的數學中,代數式 是最適合"人類手工計算的。我們可以把所有連續函數,都可以經由泰勒展開式,來把原先非線性且複雜的函數,近似成一多項式。
例如:經過泰勒展開

化簡成多項式後,又可以經過分析數學法。有時還可以把這無窮多項的多項式化簡成簡易幾項,描述起來可說是非常容易。
我們還可以注意到,再微積分中,最好積分的是單純的自然指數函數,但往往這種函數伴隨其他就會非常難積分,甚至積不出來,非得用電腦程式去跑數值分析,或用很多項的近似演算法去逼近,而這種能力是人類達不到的,甚至許多函數的積分還是電腦運算不出來的。但多項式卻沒這問題,無論是次數多大的多項式,積分完全不需用到任何特殊方法,可堪稱代數性相當大。