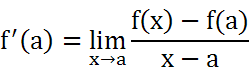
三次以上函數

三次以上函數在高中階段就比較不探討了

我們只需要大概了解其圖形即可

描點雖然可以完成呈現圖形樣貌 但也費時多了

其實我們可以找出圖形的轉折點(區域極值) 就可輕易畫出圖形

這些極值上的切線斜率為0 然而該怎麼找切線呢？ 點我

當函數上兩點非常逼近時 兩點所形成的割線即是切線

因此在( a , f(a) )上的切線斜率為：

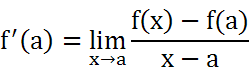
此斜率我們稱之為f(x)在a點的導數 記做f'(a)

事實上多項式函數上每一點的切線斜率皆可求出

我們稱之為導函數 記為f'(x)

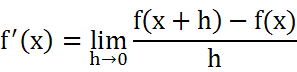
多項式函數的導函數有個簡單規則：  把次數拉到係數前面 次數減一

首先他的導函數為：

當f'(x) = 0 時 x = 1 或 x = -2

也就是圖形的極值發生在 ( 1 , f(1) )和( -2 , f(-2) ) 也就是( 1 , -4)和(-2 , 23 )

再來首項係數為正 所以圖形是由右上往左下

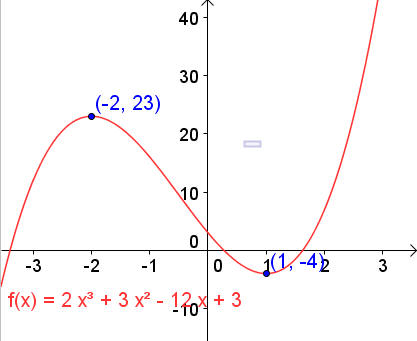
這樣是不是比一點一點找出來描點快多了呢

回首頁