§ 3－5：多項方程式
多項式方程式
（１）、n 次方程式及根的意義
設
是一個n次多項式(n為自然數)，則我們稱
為x的n次多項方程式，簡稱n次方程式。
若某個數a滿足
，則稱a是方程式的根(或解)。所謂解方程式，就是找出方程式的所有跟。
（2）、實係數多項方程式的虛根成對定理
設
為一實係數n次多項方程式，若複數z為的根，則z的共軛複數
亦為的根。
證明：因為複數z為的根，所以
因此亦為的根。
（3）、代數基本定理
n為自然數，則每一個複係數n次方程式，至少有一個複數根。
(因證明超出範圍，故略過)
推論：(a) n次方程式恰有n個根(重根須重複計算)
(b) 奇數次方的實係數多項方程是至少有一個實根
(c) 實係數方程是必可分解為若干個實係數一次式或二次式的成績
（4）、實係數多項方程式的虛根成對定理
設為實係數n次方程式，a、b為兩實數，且a<b，若
則在a,b之間至少有一實根。
舉例說明：
方程式
方程式的圖形如下
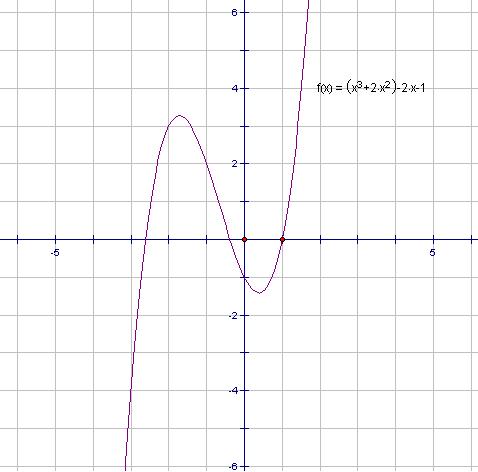
由圖來看： 方程式的一根為1，另兩根分別在[-3,-2]、[-1,0]區間內
以在[-3,-2]的根來看，
，
由定理來看：我們知道，
所以
可推得在[-3,-2]區間中有解
說明： 事實上我們要確定在[a,b]區間中是否有根的話
只要知道
與
是否是一個在x軸上方另一個在x軸下方就行了
因為
為連續函數
如果可以確定不同的兩個函數值與分布在x軸的上下各一
那麼就可以確定在這區間內必存在至少一個x使得
(既然是與分布在x軸的上下各一，那麼就可以得到
路人：講那麼多卻只有附一張圖？你不知道現在圖片已經沒甚麼看頭了嗎？
編者：是阿！我也知道現在比較流行會動的(想歪的自己去面壁XD)
所以請到互動區或者點此連結 請點我
編者：我知道這一章確實比較沉悶一點，所以附一個小遊戲給大家輕鬆一下。
請大家到互動區去或者點此連結 請點我