？
？
我們先考慮
>
>
的情形：
作
，
，然後在
邊上任取一點
，再自點作
邊的垂線，設垂足為
。
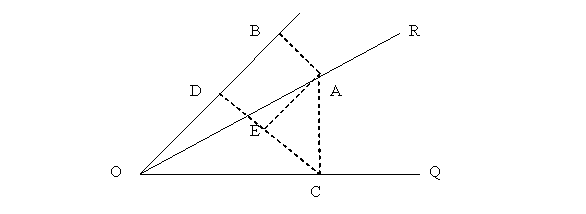
因
，所以
。
另我們自點作
的垂線，設垂足為
，再自點作
的垂線，設垂足為
，則
。
因
，故我們來看看
是否也能像
一樣可以用
與，的三角函數值來表示。
自點作
的垂線，設垂足為
，則因四邊形
為一矩形，所以
，又
（同角的餘角相等），
故
，
因此
由之得
，
，
故
？
對於任意角與，
？
因對於任意角
，恆有
，所以我們知道對於任意角與，
？
又因對於任意角，
，
，
所以由
可得
？
由正弦、餘弦函數的和角公式，可導出正切函數的和角公式：
和角公式
由和角公式，我們知道：對於任意角與，
。
因此，當=時，我們就有
。由於
，
所以
。同樣利用正弦、正切函數的和角公式，可進一步推得：
二倍角公式
， 
知道
的值，利用二倍角公式可求得
，
以及
的值。
知道的值，利用二倍角公式亦可求得
，
以及
的值。
由於=
，所以
，因此
。
另一方面，
，所以
，因此
。
由
，
，當≠
（
為任意奇數時），
綜合上述討論：
半角公式
(
取法視
)
讓我們回顧一下所介紹的和角公式，根據正弦、餘弦函數的和角公式與差角公式：對於任意角
與
，
1.
2.
3.
4.
由1.+2.得
，
由1.-2.得
，
由3.+4.得
，
由3.-4.得
，
故有：
積化和差公式
為了便於由兩正弦函數（或兩餘弦函數）的積求其和或差，我們在上述積化和差的公式中，令
，
，
則
，
。那麼前述積化和差的公式就可寫成：
和差化積公式
