三角形面積
任意畫一三角形![]() ,並自其中一頂點
,並自其中一頂點![]() 作對邊
作對邊![]() 的垂線,設垂足為
的垂線,設垂足為![]() 點。(注意:當
點。(注意:當![]()
![]() 時,
時,![]() 點與
點與![]() 點重合,
點重合,![]() =
=![]() 。)如下圖所示:
。)如下圖所示:
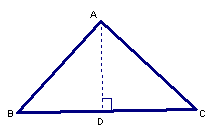
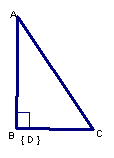
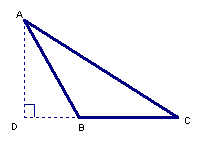
為方便起見,我們仍以![]() ,
,![]() 和
和![]() 分別表示
分別表示![]() ,
,![]() 和
和![]() 的對邊長,則
的對邊長,則![]() 。
。
因為![]() 的面積=
的面積=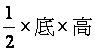 ,所以就有
,所以就有![]() 的面積=
的面積=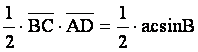 ,同理可得
,同理可得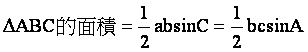 ,
,
把這些結果綜合起來,就有三角形面積公式:
|
|
由三角形面積公式,我們可以推得正弦定理:
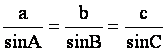
|
由正弦定理知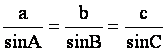 =
=![]() ,這個比值到底是多少呢?
,這個比值到底是多少呢?

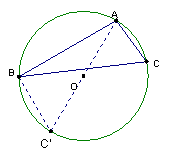
我們先做出![]() 的外接圓。由於圓內等弧所對的圓周角恆相等,我們讓三個頂點之一,
的外接圓。由於圓內等弧所對的圓周角恆相等,我們讓三個頂點之一,
例如點![]() ,在圓周上移動,當
,在圓周上移動,當![]() 點移動到
點移動到![]() 點,
點,![]() 通過圓心
通過圓心![]() 時,
時,![]() =圓
=圓![]() 的直徑,
的直徑,![]() 弧長恰為半圓,故
弧長恰為半圓,故![]() =
=![]() ,
,
因此就有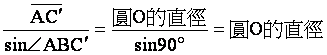 ,但在
,但在![]() 中,
中,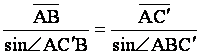 ,而
,而![]() ,
,
因此就有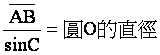 。
。
固正弦定理可進一步寫成:
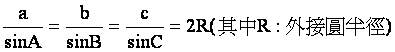 |
餘弦定理
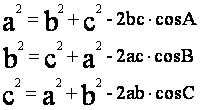 |
餘弦定理中的![]() 可以用下面方法導得:
可以用下面方法導得:
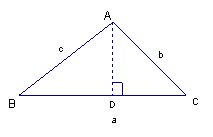
(1)當![]() 為銳角時,自A點作
為銳角時,自A點作![]() 的垂線,設垂足為
的垂線,設垂足為![]() 點,則
點,則![]() ,
,
![]() ,
,
故![]() ,在直角三角形
,在直角三角形![]() 中,我們有
中,我們有![]() ,
,
所以![]() =
=
![]()
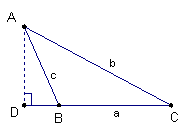
(2)當![]() 為鈍角時,同樣自
為鈍角時,同樣自![]() 點作
點作![]() 的垂線,設垂足為
的垂線,設垂足為![]() 點,
點,
則![]() ,
,![]() ,故
,故![]() ,
,
在直角三角形![]() 中,我們有
中,我們有![]() ,所
,所![]() =
=![]()
(3)當![]() 為直角,由畢氏定理知
為直角,由畢氏定理知![]() ,但因
,但因![]() ,所以
,所以
![]() 也成立。
也成立。
同理可證得:![]() ,
,![]()