三角函數的圖形

在這一節裡，我們將引進角的另一種度量單位，以便把三角函數看作實數間的對應關係，並在座標平面上描繪其圖型，研究這些函數的特性。

弧度

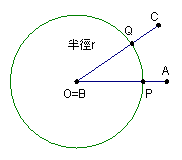
讓我們先來回顧一下，我們是怎麼量出∠ABC是多少度的？ 

由於角的大小完全由其兩邊張開的程度來決定，與其兩邊的長度是無關的。

以任意長γ為半徑畫一圓O，將其圓周等分為360格，那麼每一格的弧所對的圓心角就是1°，一個圓周角就是360°。

如果我們將∠ABC的頂點B放在圓心O上，並設其兩邊與(或其延長線)分別與圓O交於P與Q點，那麼∠ABC的度數及等於∠POQ的度數，

且，因此∠ABC=∠POQ=

(1)由於圓O的周長為，故∠ABC=∠POQ= 。在上式中，為一常數，我們規定此常數為一弧度。亦即360°= 弧度。

因此，1°= 弧度，故有

由(1)式可得

         (2)   ∠POQ= 弧度

根據(2)式可得

扇形的弧長與面積

由以上討論，我們知道：若圓O的半徑為r，P與Q為圓周上兩點，則∠POQ= 弧度。

由此可知：

設∠POQ=θ弧度，則PQ的弧長為rθ，因此PQ的弧長為圓O周長之比，

故扇形POQ面積= ×圓O的面積= π=

因此我們有

要特別注意：當我們用弧度為單位表示依角的大小時，習慣上常把〝弧度〞兩字省略不寫。

    要注意：sinπ°不可簡記為sinπ，因為根據習慣表示法，sinπ的意思是sin(π弧度)，亦即為sin180°，而非sinπ°。

三角函數的圖形及其特性

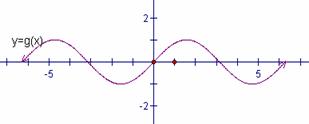
正弦函數的圖形及其特性

描繪函數圖形最直接的方法就是描點法：先求出某些特殊的值，並列表如下：

在依此標出其上的一些點，然後依次用平滑曲線將這些點連起來。

                     

函數的週期

使得對於其定義域中每一元素，恆有，

我們就稱這個函數為一週期函數。如果又可找到滿足上述性質的最小正數，我們就說這個週期函數的週期為。

由於對於任意實數，我們恆有，而且又滿足這個性質的最小正數，所以正弦函數是一週期函數，他的週期為。

正弦函數的特性

(1)正弦函數的定義域為

(2)正弦函數的值域為｜-1

(3)正弦函數的週期為

餘弦函數的圖形及其特性

我們同樣可以用描點法描繪的圖形，因為對於任意實數，恆有，

所以將正弦函數的圖形向右平移單位，即可畫出的圖形。

餘弦函數的特性

(1)餘弦函數的定義域為

(2)餘弦函數的值域為｜-1

(3)餘弦函數的週期為

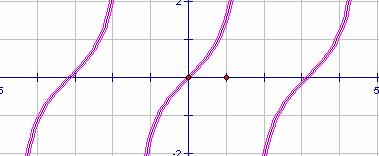
正切函數的圖形與特性

使用描點法描繪正切函數的圖形時，因為對於任意實數x，恆有，

所以我們只要描繪區間＜x＜上正切函數的圖形，然後逐次向右或向左平移π單位，即可得出的全部圖形。

(注意：時，是無意義的)

                       

正切函數的特性

(1)只有當…時，無意義；對於其他的實數x，的值都可確定，因此正切函數的定義域為x∣≠，。

(2) 正切函數的值域為R

(3)正切函數的週期為

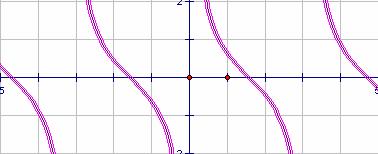
餘切函數的圖形與特性

因為對於任意實數≠，恆有，

所以我們只要將正切函數的圖形向左平移單位，再將所得的圖形對軸鏡射，

即得餘切函數的全部圖形：

餘切函數的特性

(1)只有當，…時，無意義，因此餘切函數的定義域為x∣≠，。

(2) 餘切函數的值域為R

(3)餘切函數的週期為

正割函數的圖形與特性

由倒數關係知道：當≠0時，。

因此由餘弦函數的圖形，約略可得到正割函數的圖形。

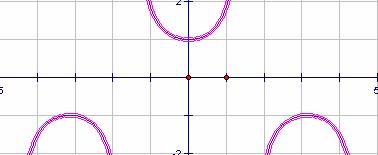
正割函數的特性

(1)正割函數的定義域為x∣≠，。

(2) 正割函數的週期為

(3)正割函數的值域為∣

餘割函數的圖形與特性

因為對於任意實數，≠，，恆有，

所以只要將正割函數的圖形向右平移單位，即得餘割函數的全部圖形。

          

餘割函數的特性

(1)餘割函數的定義域為x∣≠，。

(2)餘割函數的週期為

(3)餘割函數的值域為∣或