銳角三角函數值的定義

     相似三角形的性質中，一直角三角形某兩邊的比值，以及另一個相似直角三角形之ㄧ對應邊的邊長，即可求得另對應邊的長

直角三角形ABC(其中∠C為直角)，相異兩邊的比值有下列六個：

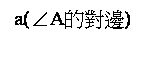
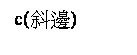
當∠A的度數為θ時，我們常用sinθ、cosθ、tanθ、cotθ、secθ與cscθ分別表示sinA、cosA、tanA、cotA、secA、cscA。

     如此一來，給定一個θ的值(0°＜θ＜90°)，則sinθ、cosθ、tanθ、cotθ、secθ與cscθ的值都隨之定，因此，它們都是θ的函數，依序稱為正弦函數、餘弦函數、正切函數、餘切函數、正割函數與餘割函數，這六個函數統稱為三角函數。

若三角形ABC中，∠C=90°，∠A的度數為θ，以 =a，=b與 =c就有

三角函數的基本關係

     倒數、商數、平方關係

  由上一節的討論，我們不難發現，這六個三角函數並非毫不相干的，他們彼此相互關聯

      此外我們還可由畢氏定理得出下述平方關係：

proof`：