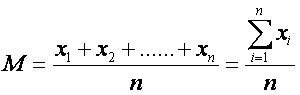
平均數─算術平均數
1.定義：
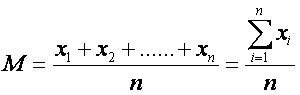
2.未分組資料：
設n個數值
，
，……，
之算術平均數，則
EX：求下列各數的算術平均數：2，3，6，7，7，8，9，9，9，10。
A：
= 7
3.已分組資料：
如果各組內的資料均勻分布於該組組距內，或集中於該組組中點
可代表組內各數的平均數，其算術平均數為
組距 |
該組中點 |
組距內的個數 |
|
|
|
|
|
|
|
|
|
… |
… |
… |
|
|
|
4.算術平均數之平移變量：
若一組資料之數值群集於A點附近且數值可能很大，則求各數值總和常因數值過大，容易導致計算錯誤或過份費時，此時宜將變量之起點平移到A點，以簡化其數值。
其平均數為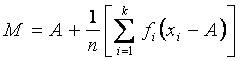
說明：
5.算術平均數之平移且縮小變量：
若分組次數表中之各組組距相等時，可將變量平移及伸縮尺寸以簡化計算。
其平均數為
，其中h為組距。
EX：100戶人口每月收入之次數分配表如下：
組別 |
30~40 |
40~50 |
50~60 |
60~70 |
70~80 |
80~90 |
90~100 |
100~110 |
人數 |
5 |
11 |
20 |
33 |
18 |
8 |
3 |
2 |
求其算術平均值。
A：
組別 |
次數 f1 |
組中點 x1 |
A=65 x1-A |
d1= |
f1d1 |
30~40 40~50 50~60 60~70 70~80 80~90 90~100 100~110 |
5 11 20 33 18 8 3 2 |
35 45 55 65 75 85 95 105 |
-30 -20 -10 0 10 20 30 40 |
-3 -2 -1 0 1 2 3 4 |
-15 -22 -20 0 18 16 9 8 |
總計 |
100 |
|
|
|
-6 |
65+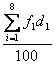
×10=65+(-6)×
=64.4
EX：甲乙兩校高二學生數學競試成績如下表，問何校成績較優？
校別 |
班別 |
人數 |
平均成績 |
甲校 |
一班 二班 三班 |
48 49 52 |
71.30 75.23 74.36 |
乙校 |
一班 二班 |
50 51 |
75.43 73.50 |
A： 甲校：
=73.66
乙校：
=74.46
乙＞甲，所以乙校成績較優。
6. 算術平均數的性質：
任一數中，各項數值與其算數平均數之差的總和為零，
說明：
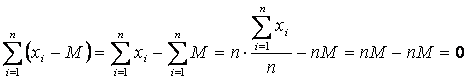
（註：算數平均數乃是各數值的重心）
7.算術平均數的適用範圍：
( i )所有資料的是數值十分集中。若所有資料的數值過份分散，則不宜採用算數平均數來代表整個全體的特性。
例如：某人一手泡在沸水中，一手浸在冰水中，我們若以算數平均數
來表示此人所受的感受，就令人啼笑皆非了。
( ii )各數值具有相等的重要性。因為算數平均數是對各項數視以同等的待遇，因此數值資料的重要程度不同，則不宜使用算數平均數。
例如：某生國文60分、英文70分、地理96分、數學100分…等。我們不能將各科視為同等的待遇，用算術平均數代表該生的平均成績，因為各科每週授課時數不同。
