定積分的概念
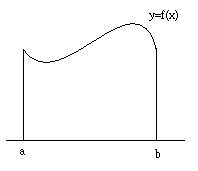
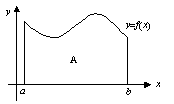
定積分的概念形成及其發展，是為了求平面面積的大小等問題。對於規則的幾何圖形，如三角形、圓形等，可利用面積公式求其面積。但對於平面上不規則的連續曲線，如y=f(x)以下，x軸以上，從x=a到x=b所為成的區域R，又當如何求其面積A呢？
我們可以仿照「曹沖稱象」之方式將要求的區域面積做切割再累加，切的愈細當然估計的愈準確。因此，接下來我們將利用下面四個步驟將所求之面積作無窮切割再累加起來求此面積。
1. 區間[a,b]分割(此作用是將求區域面積切成n個小面積)將區間[a,b]任意分割成n個子區間，亦即在a與b之間任意插入n－1個分點，使
a＝x0＜x1＜x2＜…＜xi＜…＜xn＜b
因此可得n個子區間依次為
[x0,x1]，[x1,x2]，…，[xi-1,xi]，…，[xn-1,xn]
令△xi＝xi－xi-1，表子區間[xi-1，xi]的長度，i＝1,2,…,n
令∥P∥＝Max{△x1,△x2,…,△xn}，稱為這分割的「範數」；∥P∥→0表示這分割很細，也就是說n→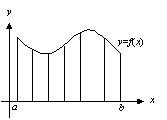
。過這些分點作平行於y軸的直線，將區域R分割成n塊小面積。
2. 選點
現從第I個子區間[xi-1,xi]中任取一點wi，i＝1,2,…,n
3. 求和
利用上面所找到的點之函數值f(wi)為高，△xi為底作一矩形，則由圖可知，此一矩形面積f(wi)•△wi與每一塊小面積大小近似
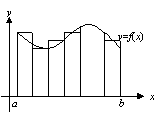
故區域R之面積A，可近似地表示成
A≒Sn＝
此式Sn＝
稱為f(x)在[
a,b]上的黎曼和(Riemann
Sum)。
4. 求黎曼何的極限
顯然可知，當∥P∥→0或即當n→
時，Sn就愈接近於區域R之面積A。換言之，當我們將區間[a,b]作無限分割 時，每一塊小面積之累加就是我們求的面積A，即A＝limSn＝lim
從上述的討論可知，求區域R的面積，可從分割、選點、求和及取極限求得。現我們可利用此概念與分析，作以下之定義。
定義1.1
設f(x)為定義於[a,b]之有界函數，a＝x0＜x1＜…＜xn為[a,b]之一分割，△xi＝xi－xi-1，wi
[xi-1,xi]，i＝1,2,…,n。若其黎曼和之極限lim
存在，且此極限值與[a,b]之分割及wi之選取無關，則稱f(x)在[a,b]在內可積分(integrable)，並將此極限值記為
，即
＝lim
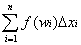
並且我們稱符號
為f(x)在[a,b]之定積分(definite
integral)，其中f(x)稱為被積函數，b與a分別稱為積分上下限，x稱為積分變數。
從上面的定義可知，可積分乃是極限問題。通常，極限有時會不存在的，故並不是每一個有界函數均為可積分。接下來的定裡要討論函數的可積性。
定理1.1
(1) 若f(x)在閉區間[a,b]上為連續，則f(x)在[a,b]是可積分的。
(2) 若f(x)在閉區間[a,b]上為單調，則f(x)在[a,b]是可積分的。
(3) 若f(x)在閉區間[a,b]上為有界，且有有限個不連續點，則f(x)在[a,b]是可積分的。
雖然我們在上面是以求面積為例，來解說定積分的意義，但積分符號”
”是由Leubbutz創造的。是英文字Sum之第一個字母S拉長的，故直觀上f(x)dx是可視為[a,b]上之點上的無窮小量，則定積分
表示[a,b]上之無窮小量f(x)dx的累加。因此，在幾何上來說，若將f(x)解釋為矩形的長，dx視為寬，則定積分是無窮多的矩形面積的累加，則可以求面積之大小。若將f(x)解釋為側面積，dx視為寬，則定積分是無窮多的小體積的累加，則可以求體積之大小。
定積分
是代表函數f(x)在[a,b]上的黎曼和極限，故它是一個確定的數，因此，這個數只決定於函數f(x)與其上下限之值，與積分變數無關。於是
＝
＝
＝…
根據定積分的定義與求區域面積的概念，故得以下定理。
定理1.2
若f(x)≧0且在[a,b]內連續，則y＝f(x)以下，x軸以上，從x＝a到x＝b所圍成的區域R的面積A為
A＝
根據定積分的定義及面積的幾何意義，我們不難推得下列之性質：
定理1.3
若f與g是在區間[a,b]的連續函數，則
(a)
＝
＋
(b)
＝c
(c是常數)
(c)
＝0
(d)
＝
＋
(c是介於a與b之間的任意數)
(e)若f(x)≧0，
x
[a,b]，則
≧0
(f)若f(x)≧g(x)，
x
[a,b]，則
≧
(h)
＝－
