微積分基本定理

在上一節裡，我們介紹的定積分的意義。也發現每次求定積分的值，如果都由分割、選點、求和、取極限四步驟完成，確實非常的困難。因而本節的目的即是要介紹利用不定積分來求定積分的方法，亦即所謂的「微積分基本定理」。此定理使許多有關求積分的問題得以迎刃而解。更重要的是它建立微分與積分的關係，由此關係可看出，微分與積分是兩個互為可逆的運算，如平方與開方。

接下來，我們先要介紹積分均值定理，我們將利用它來證明微積分基本定理。

定理2.1

(積分均值定理)

若函數f(x)在區間[a,b]上連續，則我們在a與b間至少可以找到一個數c，使得 ＝f(c)(b－a)

證明：

因為f(x)在區間[a,b]上連續，則由前述定理可知，必存在c₁,c₂ [a,b]，使得

f(c₁)≦f(x)≦f(c₂)， x [a,b]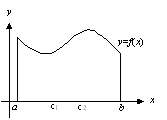　　　　　　　

再由定積分之性質(f)得　　　　　　　　　　

≦ ≦

又因f(c1),f(c2)為常數，故得

f(c₁)(b－a)≦ ≦f(c₂)(b－a)，亦即

f(c₁)≦ 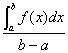≦f(c₂)

由中間值定哩，可知存在c [a,b]，

＝f(c)(b－a)                                                □

定理2.2

(微積分基本定理)

設函數f(x)在區間[a,b]上連續

(1) 若函數G(x)定義為G(x)＝ ， x [a,b]

則G’(x)＝ ＝f(x)

(2) 設F(x)為f(x)在[a.b]上之任一反導函數，則

＝F(b)－F(a)

證明：

(1)因為G(x)＝ ，現考慮自變數x有一個增量△x，且

(x＋△x) [a,b]，故

G(x＋△x)－G(x)＝ －

              ＝ ＋ －

              ＝

根據積分均值定理，上式顯然可寫為

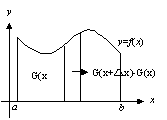
G(x＋△x)－G(x)＝g(c)△x(x＜c＜x＋△x)

即 ＝f(c)

又因為已知f(x)為連續函數，故

G’(x)＝lim ＝limf(c)＝f(x)

即f(x)是G(x)之導函數，即G’(x)＝ ＝f(x)

(2)如果我們找到另一個F(x)，使F’(x)＝f(x)，那麼F(x)可寫成

F(x)＝G(x)＋c＝ ＋c(c為任意常數)

在上式中，分別令x＝a與x＝b時，則有

F(a)＝ ＋c＝c c＝F(a) 以及

F(b)＝ ＋c＝ ＋F(a)

F(b)－F(a)＝                                            □

 一般來說，已了微積分基本定理後，若想計算一連續函數f(x)從a到b之積分，其實只需求被積函數的反導函數F(x)，然後計算F(b)－F(a)，則所求的值即為所求的定積分。而求被積函數f(x)的反導函數相當於求f(x)的不定積分 。而對於求不定積分的技巧，我們已經介紹了。此定裡也可看出它簡化了由定積分定義求定積分的繁雜計算，因而提高了定積分得實用範圍。