shape - 演算法筆記

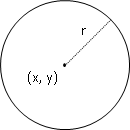
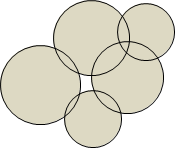
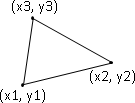
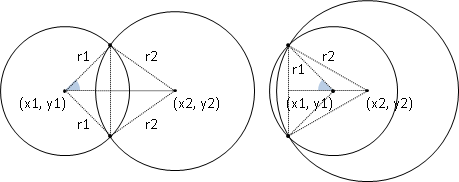rectangle

擺得很正的矩形，四個邊都平行於座標軸

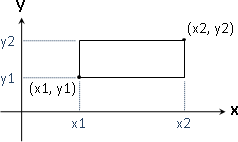
經過數學課程洗禮，大家看到矩形都是直覺想到長與寬。然而在計算學當中，我們傾向記錄左下角座標（X座標、Y座標的下界）與右上角座標（X座標、Y座標的上界）。

就算矩形退化成線段、點，這種記錄方式也不會有問題。

UVa 460 191

矩形相交

要判斷矩形相交相當麻煩，相交的情形有許多種。

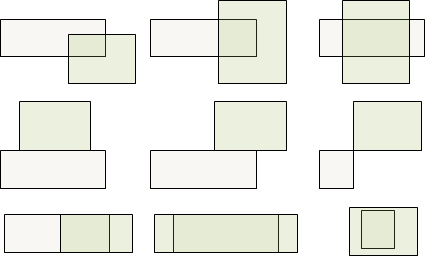
逆向思考，事情就變得容易多了：判斷矩形不相交！以第二個矩形作為基準，第一個矩形完全落在其左方、右方、下方、上方，就是不相交。

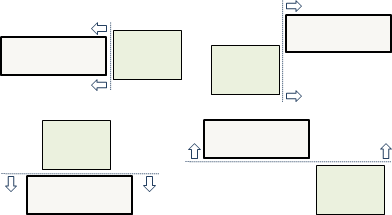
如果是空心矩形，那麼還得偵測第一個矩形是不是被第二個矩形框住，以及第二個矩形是不是被第一個矩形框住。

大量矩形交集，之一

兩個矩形的交集還是矩形（可能退化成線段、點）。運用incremental method進行推理，大量矩形的交集當然還是矩形。

採用incremental method，一次讀入一個矩形，不斷更新交集。時間複雜度O(N)，N是矩形數量。

大量矩形交集，之二

大量矩形聯集，之一

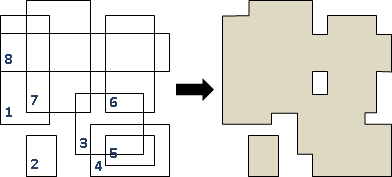
將聯集區域切割為數個矩形。採用incremental method，一次讀入一個矩形，不斷更新聯集。

下面這段程式碼僅計算聯集面積。至於聯集多邊形，就請讀者自行研究了。

struct Rectangle {int x1, y1, x2, y2;} rect[100];

// 計算a與b的差集，將差集區域切割為數個矩形
Rectangle cut[4];	// 回傳值。切割後的差集。
int divide(Rectangle a, Rectangle b)
{
	// no intersection
	if (b.x2 <= a.x1 || b.x1 >= a.x2) return 0;
	if (b.y2 <= a.y1 || b.y1 >= a.y2) return 0;

// b contains a
	if (b.x1 <= a.x1 && b.x2 >= a.x2 &&
		b.y1 <= a.y1 && b.y2 >= a.y2) return -1;

// a divides b
	// cut a into pieces
	int cuts = 0;
	if (b.x1 >= a.x1)	// cut left-side
	{
		Rectangle t = a; t.x2 = a.x1 = b.x1;
		if (t.x1 != t.x2) cut[cuts++] = t;
	}
	if (b.x2 <= a.x2)	// cut right-side
	{
		Rectangle t = a; t.x1 = a.x2 = b.x2;
		if (t.x1 != t.x2) cut[cuts++] = t;
	}
	if (b.y1 >= a.y1)	// cut buttom-side
	{
		Rectangle t = a; t.y2 = a.y1 = b.y1;
		if (t.y1 != t.y2) cut[cuts++] = t;
	}
	if (b.y2 <= a.y2)	// cut top-side
	{
		Rectangle t = a; t.y1 = a.y2 = b.y2;
		if (t.y1 != t.y2) cut[cuts++] = t;
	}
	return cuts;
}

float rectangle_union()
{
	vector<Rectangle> cur;
	for (int i=0; i<100; ++i)
	{
		vector<Rectangle> next;
		for (int j=0; j<cur.size(); ++j)
		{
			// 先求出rect[i]以外的聯集區域
			int cuts = divide(cur[j], rect[i]);
			if (cuts == 0)
				next.push_back(cur[j]);
			else if (cuts == -1)
				continue;
			else if (cuts > 0)
				next.insert(next.end(), cut, cut+cuts);
		}
		cur = next;
		// 最後再加上rect[i]本身
		cur.push_back(rect[i]);
	}

float area = 0.0;
	for (int i=0; i<cur.size(); ++i)
		area += (rect[i].x2 - rect[i].x1) *
				(rect[i].y2 - rect[i].y1);
	return area;
}

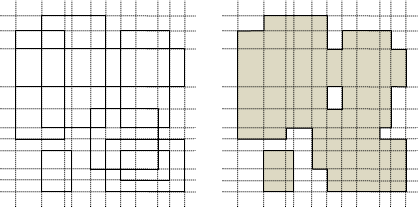
時間複雜度的分析比較特別。每次更新聯集，都會增加一些矩形、減少一些矩形，所以很難估計矩形數量。

以宏觀視角觀察矩形數量。考慮所有矩形頂點，X軸離散化、Y軸離散化，最多產生(2N-1)×(2N-1)個格子。聯集區域一定是由這些格子構成，聯集區域的格子數量一定小於等於(2N-1)×(2N-1)。更進一步，聯集區域切割出來的矩形數量，一定小於等於格子數量！

更新聯集，也就是檢查聯集區域切割出來的每一個矩形，時間複雜度O(N²)。一共更新N次，總時間複雜度O(N³)。

大量矩形聯集，之二

一、X軸離散化、Y軸離散化。O(NlogN)
　　最多產生(2N-1)×(2N-1)個小格。
二、窮舉每個小格、窮舉矩形，判斷每個小格屬於哪個矩形。O(N³)

UVa 870 221 688

大量矩形聯集，之三

一、X軸離散化，附帶矩形左右邊界資訊。O(NlogN)
二、Y軸離散化。O(NlogN)
三、每一個橫條，由左往右掃描，判斷每個小格是否在矩形裡。O(NN)
　　以矩形上下邊界，判斷其左右邊界是否穿過當前橫條。
　　遇到矩形左邊界+1，遇到矩形右邊界-1。

大量矩形聯集，之四

觀察相鄰的橫條。相鄰的橫條的聯集區域變化，與矩形的消失、出現密切相關。我們可以運用動態的資料結構，儲存第一個橫條的聯集區域，然後逐步更新每一個橫條。

一、依序處理每個橫條。
　　首先建立第一個橫條的線段樹，節點附帶sum資訊。
　　（預先離散化X軸。O(NlogN)）
二、一次做一個橫條。看看哪些矩形離開了/進來了，更新線段樹。
　　（預先離散化Y軸，附帶矩形上下邊界資訊。O(NlogN)）
三、從頭到尾總共N個矩形離開了/進來了，線段樹更新總共2N次。O(NlogN)
　　每做完一個橫條，樹根的sum就是該橫條之內的聯集區域面積總和。
　　每做完一個橫條，就將sum累加至聯集面積。

ICPC 4758

Klee's measure problem

推廣到高維度。

circle

圓形