cycle
cycle
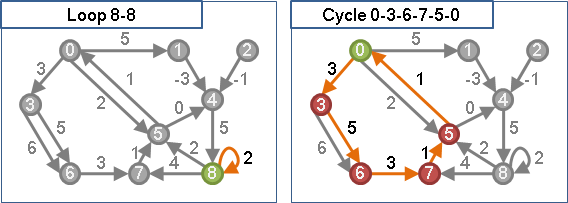
「環」。頭尾循環的路徑。大家習慣令點與邊不可重複。
loop
「自環」。一條邊,自己連向自己。
cycle
cycle
「環」。頭尾循環的路徑。大家習慣令點與邊不可重複。
loop
「自環」。一條邊,自己連向自己。

negative weight cycle
negative weight cycle(negative cycle)
「負環」。權重為負值的環,可能有許多只。
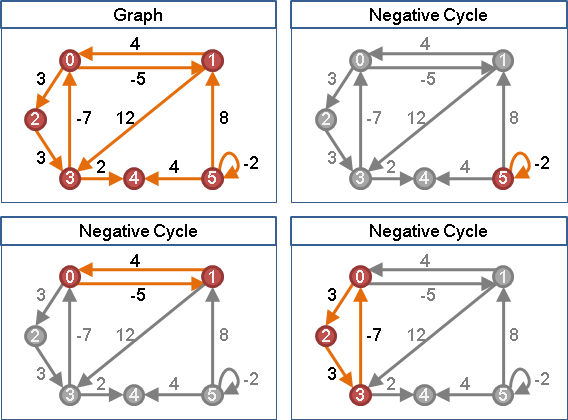
Moore's algortihm可以找出其中一個負環。時間複雜度O(VE)。
backtracking可以找出所有負環。時間複雜度O(V!)。
minimum weight cycle
minimum weight cycle(shortest cycle)(girth)
「最小環」。一張圖上權重最小的環,可能有許多只。
求最小環如同求最短路徑;求最大環如同求最長路徑。
圖上無負環,P問題。圖上有負環,NP-complete問題。
circumference:外周長。最大環。 girth:內周長。最小環。
演算法
窮舉圖上每一條邊ij: 甲、暫時拿掉邊ij,權重改成無限大。 乙、求出j點到i點的最短路徑。 丙、放回邊ij,形成一個環,即是強制經過邊ij的最小環。 丁、權重最小者即是最小環。
時間複雜度等同於求O(E)次兩點之間最短路徑的時間。
演算法
Floyd–Warshall algorithm,順手尋找最小環。
時間複雜度O(V³),空間複雜度O(V³)。
有向圖,正邊 O(V³) 有向圖,無負環 O(V³) 有向圖,有負環 不適用 無向圖,正邊 O(V³) 無向圖,無負環 不適用 無向圖,有負環 不適用
計算最小環的權重
找出一個最小環
仿效最短路徑演算法,增廣陣列空間為O(V³)。
然而這種做法實際效率不佳。這裡提供比較簡潔、效率較佳的實作方式,時間複雜度O(V⁴),空間複雜度O(V²)。
minimum ratio cycle
minimum ratio cycle
「最小比率環」。一張圖每條邊有兩組權重,第一組權重可為任意值,第二組權重不可為負值;於是一個環也有兩組權重。最小比率環是「第一組權重除以第二組權重」最小的環,可能有許多只。
已被證明是NP-hard問題。
第一個想法:搜尋答案
找出圖上所有的環,比較各個環的比率之後,就得到最小比率環了。然而,要找出圖上所有的環,是不容易的事情。
逆向思考,直接搜尋比率,再來看圖上有哪些環符合比率吧!
第二個想法:除法化作減法
令邊的兩組權重標記為w1和w2,環的兩組權重標記為∑w1和∑w2,環的比率標記為r = ∑w1÷∑w2。
我們想知道一個環的比率r是多少,也就是說我們想知道∑w1÷∑w2是多少,也就是說我們想知道∑w1會等於多少的r×∑w2──要是直接把∑w1與r×∑w2相減,亦可表示∑w1與r×∑w2的多寡關係:r太小就表示差值是正數,r剛剛好就表示差值是零,r太大就表示差值是負數。利用這種方式,原本難以分析的除法式子,就成了容易分析的減法式子了。
為了湊出這道減法式子,把原來權重為w1和w2的一條邊,改為權重為w1 - r×w2的一條邊。如此一來,環的權重就變成了∑(w1 - r×w2) = ∑w1 - r×∑w2,這就成了我們所要的減法式子。
現在只要設定好r,然後看看圖上有沒有零環,如果有零環就表示這個r是合理的比率值。新圖上的零環,就是原圖上比例為r的環。
新圖的權重 vs. 原圖的比率
設定好r之後,新圖上究竟有哪些環?
一、如果新圖上有負環:這個負環的權重∑(w1 - r×w2) = ∑w1 - r×∑w2 < 0,可推得∑w1÷∑w2 < r。也就是說找到了一個負環,比率比r還小。
二、如果新圖上沒有負環,但有零環:可推得∑w1÷∑w2 = r。由於圖上沒有負環,沒有比率比r小的環,所以這個零環就是最小比率環,r就是最小比率環的比率。
三、新圖上沒有負環、沒有零環,但有正環:可推得∑w1÷∑w2 > r。也就是說圖上所有的環,比率都比r還大。
四、新圖上沒有環:沒有環就不會有最小比率環。
至此,這個問題已變成搜尋最小比率環的比率,並判斷圖上有沒有負環的問題了。要判斷圖上有沒有負環,可以利用各種偵測負環的演算法,例如Moore's algorithm。
binary search
比率太小就有負環,比率太大就沒有負環。因此可以用binary search找答案。
演算法
一、搜尋最小比率環的比率r。使用binary search。 二、把圖上的邊的兩組權重w1和w2,改為只有一組權重w1-r×w2, 甲、圖上有負環:r太小。 乙、圖上沒負環:r太大。 丙、沒有負環、只有零環:r剛剛好。得到正解。
時間複雜度等同於偵測負環O(logR)次的時間,R是可能的比率範圍。
計算最小比率環的比率
【待補程式碼】
找出一個最小比率環
【待補程式碼】
minimum mean cycle
minimum mean cycle
「最小平均數環」。一張圖上每條邊都有權重,最小平均數環是「權重除以邊數」最小的環,可能有許多只。
最小平均數環也可以視作是最小比率環的特例,當每條邊的第二組權重都等於1的時候。
有向圖演算法(Karp's algorithm)
請參考CLRS在Bellman–Ford algorithm章節的練習題,事實上也能求出最大平均數環。用到了兩個概念:
一、圖上所有邊的權重,同時增減一數值,不影響最小平均數環的位置(但是會影響最小環的位置)。
二、單源最短路徑往外延伸,一旦碰觸到最小平均數環(或者最小環),就會不斷繞行之,讓路徑長度增加最少。此演算法採用窮舉法,求出單源最短路徑進入最小平均數環的起點。
令V為圖上的所有點構成的集合,n為圖上的點數。
圖上任意取一個點作為起點,d(k, i)為起點走k條邊到達i點的最短路徑。
d(n, i) - d(k, i)
平均權重 = min max ———————————————————
i∊V 0≤k≤n-1 n - k
如果圖不連通,可以使用Johnson's algorithm提到的技巧,新增一個起點,新增起點到圖上各點的邊,權重皆設為相同數值(例如零)。如此一來,圖上每一點都可以由起點走到,而且不影響最小平均數環的位置。
圖的資料結構為adjacency matrix是O(V³);圖的資料結構為adjacency lists是O(VE)。
計算最小平均數環的平均權重
找出一個最小平均數環
【待補程式碼】
UVa 11090
feedback edge set
feedback edge set
刪除圖上的邊,使得圖上無環。所有刪除的邊稱作feedback edge set。
無向圖:無環即是樹,minimum feedback edge set即是maximum spanning tree以外的所有邊,P問題。
有向圖:無環即是有向無環圖DAG。minimum feedback edge set是NP-hard問題。
feedback vertex set
無論無向圖還是有向圖,都是NP-hard問題。
cycle basis
cycle basis
「環基底」。環集合,加權總和可以得到圖上所有環。加法只能是xor,權重只能是0和1。
一張圖的子圖,可以表示成長度為E的01向量:0無邊、1有邊。一張圖的環,也可以如此表示。
找出一些環,當作基底,讓這些環的線性組合可以得到圖上所有環。Galois field order E。
環基底的大小是固定值E-(V-1)。
mimimum cycle basis,權重最小的環基底,P問題。
演算法目前有兩大類型,但是時間複雜度都很高。
fundamental cycle basis
「基本環基底」。以生成樹得到環基底。
一張圖上找出一棵spanning tree,剩下E-(V-1)條邊。每一條剩下的邊,各自對應一個獨一無二的環。這些剩下的邊與生成樹所形成的環,可以充作環基底,稱作「基本環基底」。
mimimum fundamental cycle basis,權重最小的基本環基底,NP-hard問題。
transmuter
用來記錄一棵生成樹的 fundamental cycle 是個類似二分圖的東西。 X側的每個點各自對應樹邊(tree edge) Y側的每個點各自對應非樹邊(cross edge) 當某個非樹邊與樹邊形成 fundamental cycle 那麼二分圖上,該樹邊到該非樹邊就有一條路徑。 也就是說一個 fundemantal cycle 中,在二分圖上所有樹邊都會連往對應的那條非樹邊。 然後二分圖有設立中繼點,以節省連接邊數(遇到完全二分圖的時候就很好用) 此偽二分圖的大小與建立時間皆為O(Eα(V))。
無向圖最小生成樹: (次小生成樹) Y側(非樹邊)標記,數值為X側鄰點( 樹邊)最小值,加入非樹邊時的best swap edge。 X側( 樹邊)標記,數值為Y側鄰點(非樹邊)最小值,刪除 樹邊時的best swap edge。 (致命邊) 無向圖最短路徑樹: 非樹邊(x,y)的數值定義為 d(s,x) + w(x,y) + d(y,t) X側( 樹邊)標記,數值為Y側鄰點(非樹邊)最小值,刪除 樹邊時的best swap edge。 (但是要小心 d(s,x)不能包含到刪除的樹邊!也就是說要注意(x,y)的方向。)