Algorithm Analysis

演算法可以切開為兩個部分：演算法設計、演算法分析。

演算法設計：製造演算法。演算法設計目前已經有一些經典手法，例如Dynamic Programming、Greedy Method等等。

演算法分析：針對特定演算法，精確計量時間複雜度和空間複雜度。演算法分析會用到很多數學知識。下面這兩本書內容很詳細，我想應該不太需要再重複整理一遍。

以下章節是隨興所至談天說地，參考看看就好。

時間複雜度、空間複雜度

要評斷一個演算法的好壞，最基本的指標是時間和空間。

最直覺的方式，就是測量程式的執行時間、程式的記憶體使用量。但是由於相同演算法於不同電腦的執行時間會有差異，又由於每個人實作演算法所採用的程式語言、程式設計技巧都不一樣，所以執行時間、記憶體使用量不是一個穩定的評斷標準。

數學家於是改為統計演算法的步驟數量、變數數量。

解決問題的成效

要評斷一個演算法的好壞，除了時間和空間的用量以外，主要還是看演算法解決問題的成效如何。

數學問題，通常可以明定解答好壞，例如數字越大越好。通常這種情況，有多種演算法可以求得正解，那麼這些演算法的成效是一樣好的。

真實世界的問題，通常難以界定絕對的好壞優劣，例如美醜、樂音噪音、喜怒哀樂、是非對錯等等，此時演算法的成效，則由人類自行判斷，利用兩兩比較、投票表決等等方式來決定成效。

Time Complexity

時間複雜度

想要描述一個演算法的效能，直覺的方式是測量演算法執行時間。但是由於執行時間深受機器規格與實作方式影響，難以放諸四海皆準，因此學術上傾向於統計演算法步驟數量。

空間複雜度與時間複雜度類似，就不多提了。

步驟數量

BUBBLESORT(A, N)                  | steps
1 for i ← 0 to N-1 do             | N
2     for j ← i to N-i-1 do       | N(N-1)/2
3         if A[j] < A[j+1] then   | N(N-1)/2
4             temp ← A[j]         | at most N(N-1)/2
5             A[j] ← A[j+1]       | at most N(N-1)/2
6             A[j+1] ← temp       | at most N(N-1)/2

total = N + 5N(N-1)/2
      = N + 2.5N² - 2.5N
      = 2.5N² - 1.5N
      = O(N²)

數學家把步驟數量寫成代數式子。例如當輸入資料有N = 1000個數字，步驟數量一共是2.5×1000² - 1.5×1000 = 2498500步。

有了步驟數量，還可以進一步粗估執行時間。假設一個步驟需要10個clock，而電腦中央處理器CPU的時脈是2GHz：每秒鐘執行2000000000個clock，那麼程式執行時間大約是2498500 × 10 ÷ 2000000000 = 0.0124925秒。

但是這不是精準的步驟數量。由於實作的關係，係數容易變動，所以係數的意義不大。因此數學家只取出代數式子的最高次方。步驟數量2.5N² - 1.5N，變成了時間複雜度O(N²)。

儘管這是非常不精準的估算方式，不過還是可以對常見的演算法進行簡易分類，粗略地比較快慢。

演算法的快慢

               | time*    | space
---------------+----------+--------
bubble sort    | O(N²)    | O(N)
insertion sort | O(N²)    | O(N)
merge sort     | O(NlogN) | O(N)
quicksort      | O(N²)    | O(N)
heapsort       | O(NlogN) | O(N)
counting sort  | O(N+R)   | O(N+R)

*worst-case

例如有兩個演算法，時間複雜度分別是O(N²)和O(NlogN)。當輸入資料有N = 1000個數字，O(N²)演算法粗估是1000²步，O(NlogN)演算法粗估是1000×10步（log₂1000 ≈ 10）。演算法的快慢相當明顯：O(N²)演算法比O(NlogN)演算法還慢！步驟數量粗估相差一百倍，執行時間粗估相差一百倍！

這種估算方式，只保留了最高次方項，還省略了係數。

因為省略了很多東西，所以這種估算方式不見得真實反映演算法的快慢。例如N = 100的情況下，O(N³)演算法可能比O(N²)演算法還快。例如兩個O(N)演算法可能不一樣快，N大則甲快、N小則乙快。

因此數學家規定N必須足夠大（類似微積分的趨近無限大）。如此一來，無論係數大小，O(N³)演算法一定比O(N²)演算法還慢，兩個O(N)演算法一定差不多一樣快。這個規定，顯然不切實際，純粹逃避現實。

然而目前尚未找到更好的方式，於是大家將就著用。

步驟數量的缺陷

現在大家採用的方式是統計演算法步驟數量。但是由於每個步驟的執行時間都不一樣，加減較快、乘除較慢，因此這也是不那麼準確的方式。

演算法步驟數量，也完全忽略了編譯器和指令流水線。演算法的實際運作過程，是將程式碼編譯成機器碼，再實施排程。CPU的指令數量、演算法的步驟數量，兩者根本沒有絕對關係。

演算法步驟數量，也完全忽略了I/O處理和記憶體管理。要是資料結構複雜一點、龐大一點，讀取資料就會變慢。

演算法步驟數量，也完全忽略了程式語言特性和平台特性。同一個演算法，用C寫執行較快，用Java、Python寫執行較慢。因為後者的記憶體管理機制更加複雜，而且牽扯到系統運作架構。

演算法步驟數量再怎麼不可靠，也比不上演算法實作的不可靠。同一個演算法，不同人寫出來的程式碼，執行效率都不一樣，相差十倍都有可能。

然而目前尚未找到更好的方式，於是大家將就著用。

步驟數量的規定

古人定義演算法，規定計算步驟數量是必須是有限步，不是無限步。用程式語言的術語來說就是：演算法不能有無窮迴圈。

古人當初規定有限步，是為了方便統計總步數。但是實務上，很多電腦程式是開啟之後就保持執行狀態，直到當機、重開機，例如網路傳輸的演算法。因此實務上可以是無限步。

輸入順序

輸入資料常常影響時間複雜度。舉例來說，當輸入資料已經排序完畢，此時實施排序演算法，只需檢查一遍輸入資料，即可發現根本無須排序，直接結束演算法，時間複雜度O(N)！

當輸入資料很整齊，那我們可以得到最佳或最壞的時間複雜度是多少；當輸入資料很雜亂，那我們可以得到平均的時間複雜度是多少。例如Quicksort，最佳O(N)，平均O(NlogN)，最差O(N²)。

一種輸入順序，得到一種時間複雜度。觀察每一種輸入順序，得到每一種時間複雜度。最小值／最大值／平均值，即是最佳／最壞／平均時間複雜度。

best-case complexity：找到最佳的輸入順序。時間複雜度的最小值。
worst-case complexity：找到最壞的輸入順序。時間複雜度的最大值。
average-case complexity：統計每一種輸入順序。時間複雜度的平均值。

計算順序

古人定義演算法，規定計算順序必須是固定的，不是隨機的。但是實務上，以隨機的計算順序，可以緩和最壞的輸入順序。

含有隨機的計算順序的演算法，必須運用機率來分析時間複雜度。一種計算順序，對應一個時間複雜度；考慮每一種計算順序的出現機率，求得時間複雜度的期望值。

Amortized Analysis

multipop stack

一個stack，一開始是空的。它有三種操作：

1. push(x)      存入一筆資料。如果stack是滿的就馬上停止。
                worst time O(1)
2. pop()        取出一筆資料。如果stack是空的就馬上停止。
                worst time O(1)
3. multipop(k)  連續取出k筆資料。如果stack是空的就馬上停止。
                worst time O(min(n,k)) 當stack有n個元素

請問進行N次操作的總時間複雜度是多少？假設空間足夠大。

我們不知道每次的操作是哪一種。可能是三種其中一種。

普通的分析

乍看之下，multipop(k)花費最多時間。我們以multipop(k)的視角，計算時間複雜度。

multipop(k)的時間複雜度是O(min(n,k))，n是當下的資料數量，k是欲取出的資料數量。因為n和k最大可到N，min(n,k)最大可到N，所以時間複雜度是O(N)。

multipop(k)最多實施N次，總時間複雜度是O(N²)。

均攤分析

N次操作，最多存入N筆資料。即是N次push()。

N次操作，最多取出N筆資料。無論pop()或multipop(k)。

N次操作，最多存取2N筆資料。無論哪種操作。

N次操作，總時間複雜度是O(2N) = O(N)。

均攤時間複雜度

一次操作，均攤時間複雜度是O(1)。

順帶一提，multipop(k)的時間複雜度是O(min(n,k)) = O(N)。multipop(k)的均攤時間複雜度是O(1)。

均攤分析的經典應用

字串搜尋Morris–Pratt Algorithm、凸包Graham's Scan與Andrew's Monotone Chain、二元搜尋樹Splay Tree。

其他主題

Amortized Analysis：步驟數量不固定，採取累計的方式。

Smoothed Analysis：分析輸入順序有多少機率是整齊的、多少機率是雜亂的。

Competitive Analysis：步驟數量、輸入順序不固定，運用機率來分析時間複雜度。

Complexity Notation

符號讀做big O，意義讀做order，用來表達上限，省略係數。

Ω下限。O上限。Θ同時滿足下限與上限（剛剛好）。

例如f(n) = 3n²+2n+1是Ω(n²)也是Ω(n)也是Ω(1)。

例如f(n) = 3n²+2n+1是O(n²)也是O(n³)也是O(n⁴)。

例如f(n) = 3n²+2n+1是Θ(n²)。

f(n) = Ω(g(n))  ⟺  f(n) ≥ c ⋅ g(n) for any constant c
f(n) = O(g(n))  ⟺  f(n) ≤ c ⋅ g(n) for any constant c
f(n) = Θ(g(n))  ⟺  f(n) = c ⋅ g(n) for any constant c

符號使用方式違反數學常識。按照常識是O(f(n)) = n²，此處卻是f(n) = O(n²)。

另外還想強調一件事：Ω、O、Θ跟best-case、worst-case、average-case沒有關係！不知道為什麼很多人認為它們相同。

符號讀做little O，用來表達上級（不含同級），省略係數。

ω下級。o上級。

例如f(n) = 3n²+2n+1是ω(n)也是ω(1)。

例如f(n) = 3n²+2n+1是o(n³)也是o(n⁴)。

f(n) = ω(g(n))  ⟺  f(n) > c ⋅ g(n) for all constant c
f(n) = o(g(n))  ⟺  f(n) < c ⋅ g(n) for all constant c

實際使用方式，採用反面觀點。

例如O(n²)是f(n) = an²+bn+c或f(n) = an+b或f(n) = a。

例如o(n²)是f(n) = an+b或f(n) = a。

例如Ω(n²)是f(n) = an²+bn+c或f(n) = an³+bn²+cn+d或更高級別。

例如ω(n²)是f(n) = an³+bn²+cn+d或更高級別。

其他函數

方才只提到多項式函數。事實上還有其他函數。

例如f(n) = log(n)，介於f(n) = a到f(n) = an+b。

例如f(n) = sqrt(n)，介於f(n) = log(n)到f(n) = an+b。

函數類型無窮無盡，無法盡數介紹。

符號讀做tilde O，意義讀做soft order，用來隱藏polylog。

Õ(g(x)) = O( g(x) logᵏg(x) ) = O( g(x) polylog g(x) )
polylog(x) = logᵏx

log*

符號讀做log star，意義讀做iterated logarithm。

不斷算log，直到變成1，總共需要的log次數。

α(n)

Ackermann function f(n,n)的反函數。實務上與常數無異。

O(𝓜(n))

多項式乘法的時間複雜度。

多項式乘法是其他多項式運算的根基。因為各種多項式運算大量使用多項式乘法，所以特地簡寫成𝓜(n)，增加可讀性。

O(n^ω)

矩陣乘法的時間複雜度。

因為數值持續刷新，而且很難背，所以用ω代替實際數值。

普通的演算法是3，最佳紀錄是2.3728596，極限是2（矩陣元素n²個，至少都要存取一次）。

Type of Computation

計算方式

現今流行的計算機，是由邏輯電路組成，使用AND與OR，兜出加減乘除四則運算。

除了邏輯電路以外，其實還有其他方式，諸如Quantum Computing、Optical Computing、DNA Computing。這些計算方式，運算能力極強，計算時間極短。之所以不流行，是因為計算難以控制、機器難以量產。

一旦新的計算方式開始流行，我們現在習慣使用的時間複雜度分析方式，只能作古了。

當今電腦計算能力的極限

也許各位已經聽聞過千禧年大獎難題之一「P = NP問題」。遇到NP問題，就得耗費大量計算時間，無法迅速求得答案。

目前的電腦，計算能力差強人意。絕大多數的問題都沒辦法快速地求解。就算找來大量電腦實施平行計算，依然沒辦法快速地求解。

然而，現代人類對於電腦有著神祇般的依賴，各種日常生活問題都祈望電腦能夠幫上忙。於是近似演算法出現了，用來求得一個馬馬虎虎差不多的答案。

數學與計算學

數學是以基本元件來構築事物、表達概念。而數學家藉由數，嘗試構築每一件事物、表達每一個概念，拼湊出世界的全貌。比如位置、形狀、關係、轉換、遞迴、極限、比較、排列、正反、假設，這些東西都是數。又比如有、無、聚、散、疏、密、盈、虧、彎、直、交、錯、動、靜，這些東西也都是數。與物體的行為有關的數，就是物理；與物質性質變化有關的數，就是化學；與生命運作有關的數，就是生物學。繼續細分下去，我們所知的各種東西，其實皆可說是數。

在數當中，可以用數量來表示的，便可以計量。像是情緒、風格、謀略，難以用數量來表示，也就難以計量，甚至不可計量。像是動作、旋律、次序，可以部分地或完全地用數量表示，便得以計量。計算學是以數量來構築事物、表達概念。而計算學家藉由數量，嘗試量度各種事物、各種概念，掌握其確切的程度與層次。

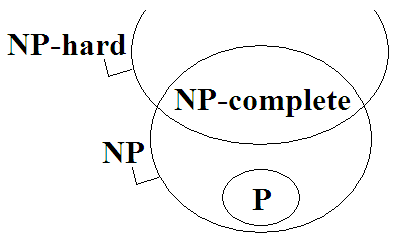
NP-complete

示意圖

更豐富的示意圖

P問題

用多項式時間演算法能夠計算答案的問題。

「找出一群數字當中最大的數字」是P問題。

P的全名是Polynomial time，定義源自於「自動機理論」，頗複雜，此處省略之。通常以「P」表示所有P問題構成的集合。

NP問題

用指數時間演算法能夠計算答案的問題，同時，用多項式時間演算法能夠驗證答案的問題。

由於P問題也可以改用指數時間演算法計算答案、當然可以用多項式時間驗證答案，故P問題都屬於NP問題。

「找出一張圖的一條Hamilton Path」是NP問題。

計算答案：
窮舉所有可能的路線，一條一條驗證。
是指數時間演算法。

驗證答案：
給定一條可能的路線，就照著路線走，看看能不能走到每一點。
是多項式時間演算法。

「找出一張圖成本最小的那條Hamilton Path」不是NP問題。

計算答案：
窮舉所有可能的路線，一條一條驗證。
是指數時間演算法。

驗證答案：
就算給定一條可能的路線，
還是必須窮舉所有路線，一條一條驗證，才知道哪條路線成本最少。
是指數時間演算法。

值得一提的是，每一個NP問題，都可以設計出多項式時間演算法，轉換成另一個NP問題。換句話說，所有NP問題都可以用多項式時間演算法彼此轉換。

NP的全名是Non-deterministic Polynomial time，定義源自於「自動機理論」，頗複雜，此處省略之。通常以「NP」表示所有NP問題構成的集合。

NP-complete問題

所有NP問題當中，最具代表性、層次最高、最難的問題。

NP-complete問題的各種特例，涵蓋了所有NP問題。只要有辦法解決NP-complete問題，就有辦法解決NP問題。

各個NP-complete問題都等價、都一樣難，可以用多項式時間演算法彼此轉換。現今已經找出上百個NP-complete問題了。

Complete的意義為：能夠代表整個集合的子集合。舉例來說，它就像是一個線性空間（linear space）的基底（basis）。

「判斷一張圖是否存在Hamilton Path」已被證明是NP-complete問題。

NP-hard問題

用多項式時間演算法轉換NP問題所得到的問題，同時，必須是跟NP-complete問題一樣難、還要難的問題。

NP-hard問題可能是：甲、NP-complete問題（是NP問題），乙、超出NP問題的複雜度，是更難的問題。

「找出一張圖成本最小的Hamilton Path」是NP-hard問題。

由「找出一張圖的一條Hamilton Path」這個NP問題，
用多項式時間把每條邊加上成本而得。
而且「找出一張圖成本最小的Hamilton Path」至少比NP-complete問題還難。

介於P與NP-complete之間的問題

為什麼學校老師要教NP-complete？

台灣的演算法課程，都是直接抄舊書，特別強調NP-complete，特別強調問題之間的轉換。不過職場上幾乎不會用到這些知識。學術上要解決P = NP問題，也不會用到這些知識。

現在比較新的教學資料，都是直接介紹多項式時間和指數時間的差異，而不是去介紹P、NP、NP-complete、NP-hard到底誰包含誰。

Weakly NP-complete

Pseudo-polynomial Time

即便是NP-complete問題，當輸入資料的數字都很小，還是可能擁有快速的演算法。

「一堆整數，從中挑出一些，總和為0」是NP-complete問題。

總共N個數字，窮舉2ᴺ種數字組合方式，一一計算總和，判斷是不是零，那麼時間複雜度是O(2ᴺN)。再考慮數字大小為K位數，那麼時間複雜度是O(2ᴺNK)。

然而，當數字大小R很小，得以利用Dynamic Programming。表格大小為RN格，將各種組合方式記載於表格。每讀取一個數字，就更新整個表格，那麼時間複雜度是O(RNN)。再考慮數字大小為K位數，那麼時間複雜度是O(RNNK)。

R其實是2ᴷ，O(RNNK)其實是O(2ᴷNNK)，只不過K很小。外觀是多項式時間，實際執行也是多項式時間，本質卻是指數時間，因此稱作「偽多項式時間」。

Weakly NP-complete問題、Strongly NP-complete問題

NP-complete問題，可以達到偽多項式時間者，稱作Weakly NP-complete問題；反之稱作Strongly NP-complete問題。

「一堆整數，從中挑出一些，總和為0」是Weakly NP-complete問題。
「判斷一張圖是否存在Hamilton Path」是Strongly NP-complete問題。

NP-complete、NP-hard並不是好的分類方式，導致事情很複雜。我真的不想介紹NP-complete。但是教科書都這樣教，我也只好配合一下。

P versus NP

P = NP ?

這是計算機科學的一個懸案。大意是說：到底NP問題能不能用多項式時間演算法解決呢？如果可以的話，那麼NP問題就都變成了P問題了。

解決這個懸案的一種方向：嘗試發明一個多項式時間演算法，解決某一個NP-complete問題（所有NP問題當中最複雜的問題）。接著將此NP-complete問題進行特例化得到所有NP問題。如此一來，所有NP問題都可以用此多項式時間演算法算出答案了。

很多人聲稱自己已經成功證明了，但是至今還沒有一個讓所有人都信服的證明：

一個演算法的時間複雜度下限

演算法教科書，都會提及時間複雜度上限O函數，但是鮮少提及時間複雜度下限Ω函數。比方說最短路徑問題，Dijkstra演算法是O(N²)，Floyd–Warshall演算法有三個迴圈是O(N³)，大家肯定耳熟能詳。但是Dijkstra演算法的時間複雜度下限是多少呢？其實也是Ω(N²)。由於上下限一樣，可以進一步寫成Θ(N²)。

Dijkstra演算法是確定性演算法，每個步驟都是確定的、固定的，所以時間複雜度上限和下限是一樣的，沒有特地討論的必要。

一個問題的時間複雜度下限

最短路徑問題，Dijkstra演算法是O(N²)，再使用priority queue則降低至O(ElogE)，有各式各樣的手段可以降低時間複雜度上限。但是最短路徑問題的時間複雜度下限至少是多少呢？演算法教科書沒講！原因是下限非常難以證明。

想要證明上限，只需想出一個時間複雜度更低（更快）的演算法，便得到新的上限、更低一點的上限。

想要證明下限，必須窮舉所有可能的演算法，證明沒有任何時間複雜度更低（更快）的演算法，才得到新的下限、更高一點的下限。

「挑選一個」與「窮舉全部」的差別，這就是困難所在之處。

能夠證明時間複雜度下限的問題

目前只有少數幾個問題，內容簡單、具有嚴格限制的問題，可以明確證明下限：

一個經典的問題是「排序一串數字」，嚴格限制「只能兩兩比較數字」。兩兩比較至少logN!次，時間複雜度下限是Ω(logN!)。

證明方式是用樹狀圖展開所有可能性，樹的末端節點共N!個，樹的高度至少是logN!。

然而，排序演算法還有counting sort、hashing這些可能性，不一定只能兩兩比較。限制成兩兩比較，非常不切實際。

另一個經典的問題是「求出一群點的凸包」。化作排序問題，得到時間複雜度下限是Ω(logN!)。

然而，要是解除了兩兩比較的限制，便有時間複雜度更低的演算法。設定這種限制，非常不切實際。

例子少得可憐。現況就是如此。

順帶一提，由於logN! = Θ(NlogN)，時間複雜度下限Ω(logN!) = Ω(Θ(NlogN)) = Ω(NlogN)。

P = NP ?

P = NP問題的困難之處，在於證明時間複雜度下限。必須證明NP問題的時間複雜度下限，到底是和P一樣是多項式時間、或者是和NP-complete一樣是指數時間。超級難的！

另一種策略是改為證明NP問題的時間複雜度上限。只要找到任何一個多項式時間演算法解決任何一個NP-complete問題，就能確確實實的降低所有NP問題的上限。不過目前也沒有人找到這樣一個演算法。

Complexity Class

複雜度分類方式還滿多的。大家一直搞不定P = NP問題，於是大家不停深入鑽研細節，於是大家順手發明了一大堆分類。一般人不需要知道這些小細節，然而你現在還是見到了。

PTIME / PSPACE / EXPTIME / EXPSPACE  時間用量、空間用量
NC⁰ / AC⁰ / ACC⁰                     邏輯閘用量

P     判定問題
#P    計數問題
PP    機率判定問題

Approximation Algorithm

APX   有多項式時間演算法
      近似到 MINOPT⋅n 或者 MAXOPT⋅n 對於一個n

PTAS  有偽多項式時間演算法 (n的多項式，ε視作定值)
      近似到 MINOPT⋅(1+ε) 或者 MAXOPT⋅(1-ε) 對於所有ε

FPTAS 有多項式時間演算法 (1/ε和n兩種變數構成的多項式)
      近似到 MINOPT⋅(1+ε) 或者 MAXOPT⋅(1-ε) 對於所有ε

Randomized Algorithm

BPP   有多項式時間演算法
      出錯機率不超過1/2，正確機率至少1/2。
      執行 k 次，投票表決，讓出錯機率不超過 (1/2)ᵏ

RP    有多項式時間演算法
      當答案為Yes，有1/2機率出錯。
      當答案為No，絕對不會出錯。
      執行 k 次，投票表決，讓出錯機率降為 (1/2)ᵏ

ZPP   有多項式時間演算法
      要嘛回答正確答案，要嘛不知道答案，機率各1/2。

Algorithm Class

Offline Algorithm / Online Algorithm

「離線演算法」是一口氣輸入所有資料之後，才能開始運行的演算法。例如Bubble Sort。

「在線演算法」是不需等待所有資料到達，就可以分時分段處理輸入的演算法。例如Insertion Sort。

有些「在線演算法」甚至可以即時提供目前所有輸入的正確輸出。例如Insertion Sort。

Static Algorithm / Dynamic Algorithm

「靜態演算法」是無法隨時修改、增加、減少原本的輸入資料，無法隨時查詢輸出的演算法。例如Dijkstra's Algorithm。

「動態演算法」是可以隨時修改、增加、減少原本的輸入資料，可以隨時查詢輸出的演算法。例如Binary Search Tree。

Exact Algorithm / Approximation Algorithm

「精確演算法」是計算結果絕對正確的演算法。

「近似演算法」是計算結果擁有誤差的演算法。

有許多問題無法快速計算正確答案。為了追求速度，就會設計「近似演算法」。

Deterministic Algorithm / Randomized Algorithm

「確定性演算法」是計算步驟順序固定的演算法。

「隨機化演算法」是計算步驟順序隨意的演算法。

輸入資料順序有時過於極端。為了追求均衡，就會設計「隨機化演算法」。

Open Problem

「懸案」。目前還沒有人知道正確答案的問題。

Open Problem Garden
The Open Problems Project
Egres Open
10000个科学难题·数学卷
List of unsolved problems in mathematics

Intractable Problem

「難題」。難以設計快速的演算法。

Tractability: Practical Approaches to Hard Problems

實務上的解法有：

一、數學規劃。請參考「Integer Programming」。
二、狀態空間搜尋。請參考「State」。
三、人工神經網路。請參考「Neural Network」。

以下做了簡單分類。注意到這不是公認的分類方式。

[Picking]
Boolean Satisfiability Problem：設定真假值，使邏輯計算式結果為真。

[Partitioning]
Partition Problem：一群數字，分成兩群，讓兩群總和一樣多。
Integer Factorization：一個數字乘積，拆散成數字。

[Packing]
Packing Problem：使用特定幾何圖形，互不重疊，盡量填滿空間。
Knapsack Problem：一個容器，一堆物品，盡量放進所有物品。
Bin Packing Problem：一堆容器，一堆物品，使用最少容器，放進所有物品。
Container Loading Problem：3D長方體堆積。
Box Stacking Problem：3D無蓋箱子堆疊。

[Covering]
Covering Problem：使用特定幾何圖形，覆蓋空間，數量盡量少。
Set Cover Problem：一堆集合，各自包含某些元素。用最少個集合，涵蓋所有元素。
Steiner Tree Problem：使用線條，連接所有地點，長度盡量短。
Facility Location Problem：選定P點，連接所有地點，成本盡量小。

[Scheduling]
Hamilton Path：拜訪所有景點的最短路線。
Vehicle Routing Problem：從起點出發多次，拜訪所有景點的最短路線。
Scheduling Problem：工廠進行生產製造、規劃最佳流程。
Graph Coloring：地圖相鄰區塊填入不同顏色，顏色種類盡量少。
Chess Problem：給定棋盤盤面，找到贏棋下法。